Superselection Rules - Philsci
... nature and scope of possible measurements”. The concept of SSR should be contrasted with that of an ordinary selection rule (SR). The latter refers to a dynamical inhibition of some transition, usually due to the existence of a conserved quantity. Well known SRs in Quantum Mechanics concern radiativ ...
... nature and scope of possible measurements”. The concept of SSR should be contrasted with that of an ordinary selection rule (SR). The latter refers to a dynamical inhibition of some transition, usually due to the existence of a conserved quantity. Well known SRs in Quantum Mechanics concern radiativ ...
Quantum Solutions For A Harmonic Oscillator
... Since a1 ≠ a2, the matrix element must vanish. This theorem will be extremely useful in applying symmetry to assist in obtaining wavefunctions. It also begins to show the importance of matrix elements in quantum mechanics. As a follow up, consider the harmonic oscillator problem Hˆ = − ...
... Since a1 ≠ a2, the matrix element must vanish. This theorem will be extremely useful in applying symmetry to assist in obtaining wavefunctions. It also begins to show the importance of matrix elements in quantum mechanics. As a follow up, consider the harmonic oscillator problem Hˆ = − ...
PPT - University of Washington
... The classic proposal by Loss and DiVincenzo involves using individual electron spins. Another proposal by Levy calls on using a two spin system. The |01>_p state is |0>_L, and |10>_p is |1>_L. ...
... The classic proposal by Loss and DiVincenzo involves using individual electron spins. Another proposal by Levy calls on using a two spin system. The |01>_p state is |0>_L, and |10>_p is |1>_L. ...
Quantum Mechanics in the Early Universe
... Settings of detectors We can now form the C observable and check whether Bell’s inequalities are violated. Quantum mechanics allows a violation of up to a factor of In this model we indeed get such a violation. This proves that the variable determining the type of hotspot we have is quantum. ...
... Settings of detectors We can now form the C observable and check whether Bell’s inequalities are violated. Quantum mechanics allows a violation of up to a factor of In this model we indeed get such a violation. This proves that the variable determining the type of hotspot we have is quantum. ...
File - Chemistry 11 Enriched
... understand the location of electrons, we must now look at the atom in three dimensions rather than the planetary early model of the atom. The orbitals are not two dimensional tracks like railroads circling an atom, but are rather areas of three dimensional space where we expect to find the electron. ...
... understand the location of electrons, we must now look at the atom in three dimensions rather than the planetary early model of the atom. The orbitals are not two dimensional tracks like railroads circling an atom, but are rather areas of three dimensional space where we expect to find the electron. ...
Heisenberg, Matrix Mechanics, and the Uncertainty Principle Genesis
... and hence as many mutually orthogonal eigenvectors “pointing” along different independent directions in the linear vector space. Again, just as we have unit vectors êx , êy , êz along the Cartesian axes, we can normalize each eigenvector to have unit magnitude. From êx and êy we can form the li ...
... and hence as many mutually orthogonal eigenvectors “pointing” along different independent directions in the linear vector space. Again, just as we have unit vectors êx , êy , êz along the Cartesian axes, we can normalize each eigenvector to have unit magnitude. From êx and êy we can form the li ...
Presentazione di PowerPoint
... Cazzaniga took her pupils to a laboratory run by Milan University's physics department. There they took part in their first particle physics experiment to study the tracks left by alpha particles in a cloud chamber. A total of three scientists, six secondary school teachers and seven classes were in ...
... Cazzaniga took her pupils to a laboratory run by Milan University's physics department. There they took part in their first particle physics experiment to study the tracks left by alpha particles in a cloud chamber. A total of three scientists, six secondary school teachers and seven classes were in ...
Quantum Computing
... Quantum computing machines enable new algorithms that cannot be realised in a classical world. ...
... Quantum computing machines enable new algorithms that cannot be realised in a classical world. ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 15. What is nanofiltration? Explain the working principle. PART - C Answer any FOUR questions (4 x 12.5 = 50) 16. Explain the formation of Quantum dots,Quantum wells and Quantum wires on the basis of Quantum mechanical approach. 17. Discuss the electronic band structure of nano crystals and solids u ...
... 15. What is nanofiltration? Explain the working principle. PART - C Answer any FOUR questions (4 x 12.5 = 50) 16. Explain the formation of Quantum dots,Quantum wells and Quantum wires on the basis of Quantum mechanical approach. 17. Discuss the electronic band structure of nano crystals and solids u ...
Quantum Computers
... Power of Algorithms Multiplication Algorithms assist in large computations Quantum Algorithms can speed up processes by using logic instructions such as `... and now take a superposition of all numbers from the previous operations...'; ...
... Power of Algorithms Multiplication Algorithms assist in large computations Quantum Algorithms can speed up processes by using logic instructions such as `... and now take a superposition of all numbers from the previous operations...'; ...
Lecture02
... • For a system with f degrees of freedom, the many particle wavefunction is formally: ...
... • For a system with f degrees of freedom, the many particle wavefunction is formally: ...
Course Syllabus
... partitioned into two because of “practical” reasons. Note: Elementary aspects of wave mechanics are assumed to be part of your background. (The first Homework assignment deals with standard one-dimensional problems.) Sakurai assumes that you have this background (he also assumes that you are familia ...
... partitioned into two because of “practical” reasons. Note: Elementary aspects of wave mechanics are assumed to be part of your background. (The first Homework assignment deals with standard one-dimensional problems.) Sakurai assumes that you have this background (he also assumes that you are familia ...
Introduction Slides
... though the quantization in units remains very important It appears to predict the atom would radiate all the time from the orbiting electron The atom does not “look” like this it is not a small “point” electron in a classical orbit ...
... though the quantization in units remains very important It appears to predict the atom would radiate all the time from the orbiting electron The atom does not “look” like this it is not a small “point” electron in a classical orbit ...
Document
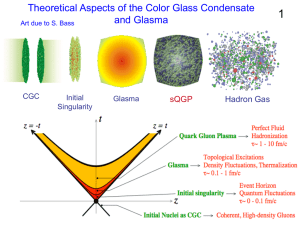
... What is the Color Glass Condensate? Glue at large x generates glue at small x Glue at small x is classical field Time dilation -> Classical field is glassy High phase space density -> Condensate Phase space density: Attractive potential ...
... What is the Color Glass Condensate? Glue at large x generates glue at small x Glue at small x is classical field Time dilation -> Classical field is glassy High phase space density -> Condensate Phase space density: Attractive potential ...
Document
... • The state of a quantum system is conditioned on the outcome of probing measurements. • States in the past are (now) conditioned on measurements until the present the past quantum state. • Past states make more accurate predictions, e.g., for: state assignment, guessing games, parameter estimatio ...
... • The state of a quantum system is conditioned on the outcome of probing measurements. • States in the past are (now) conditioned on measurements until the present the past quantum state. • Past states make more accurate predictions, e.g., for: state assignment, guessing games, parameter estimatio ...
Higgs - Transcript - the Cassiopeia Project
... field goes to zero, and Feynman’s “condition in space” disappears. But the Higgs Field is different in this respect. It still has a value – a physical reality -- at every point in space even without a source to generate it. So there really is no “empty space” anywhere. The entire cosmos is saturated ...
... field goes to zero, and Feynman’s “condition in space” disappears. But the Higgs Field is different in this respect. It still has a value – a physical reality -- at every point in space even without a source to generate it. So there really is no “empty space” anywhere. The entire cosmos is saturated ...
3.3 Why do atoms radiate light?
... description they would always radiate light and thus be destroyed). This classical explanation results from the wrong picture, that the electron is moving through the orbital, leading to a steady change in the dipole moment. • Each state, which is not an Eigenstate of the Hamiltonian has a non infin ...
... description they would always radiate light and thus be destroyed). This classical explanation results from the wrong picture, that the electron is moving through the orbital, leading to a steady change in the dipole moment. • Each state, which is not an Eigenstate of the Hamiltonian has a non infin ...
Heisenberg, Matrix Mechanics, and the Uncertainty Principle 4
... would represent such observables (as their eigenvalues are real). If the result of a measurement is a certain eigenvalue, the corresponding eigenvector represents the state of the system immediately after the measurement. The act of measurement is taken to 'collapse' the state of the systenl to that ...
... would represent such observables (as their eigenvalues are real). If the result of a measurement is a certain eigenvalue, the corresponding eigenvector represents the state of the system immediately after the measurement. The act of measurement is taken to 'collapse' the state of the systenl to that ...
投影片 1
... what people could image in ordinary life ! What is more surprising is : we human beings can “understand” this strange world ?! ...
... what people could image in ordinary life ! What is more surprising is : we human beings can “understand” this strange world ?! ...