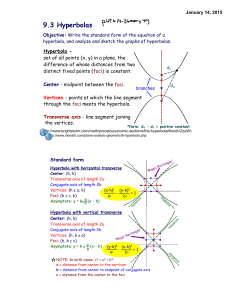
Lecture 4 Coord Geom.key
... The greatest progress in the study of conics by the ancient Greeks is due to Apollonius of Perga (died c. 190 BC), whose eight-volume Conic Sections or Conics summarized and greatly extended existing knowledge. Apollonius's major innovation was to characterize a conic using properties within the pla ...
... The greatest progress in the study of conics by the ancient Greeks is due to Apollonius of Perga (died c. 190 BC), whose eight-volume Conic Sections or Conics summarized and greatly extended existing knowledge. Apollonius's major innovation was to characterize a conic using properties within the pla ...
Final Exam Review Summer 08
... ______________ crosses or touches ______________ crosses or touches ...
... ______________ crosses or touches ______________ crosses or touches ...
pre-calculus - Chagrin Falls Schools
... Factoring – GCF, reverse FOIL, difference of two squares, sum/difference of two cubes Quadratic Formula Graphing – lines, parabolas Add/Subtract Fractions – common denominator Multiply/Divide Fractions – factor and cancel Similar Triangles – corresponding angles congruent, corresponding ...
... Factoring – GCF, reverse FOIL, difference of two squares, sum/difference of two cubes Quadratic Formula Graphing – lines, parabolas Add/Subtract Fractions – common denominator Multiply/Divide Fractions – factor and cancel Similar Triangles – corresponding angles congruent, corresponding ...
Chapter 2.2
... Sandwich Theorem Revisited Infinite Limits as x→a End Behavior Models Seeing Limits as x→±∞ ...
... Sandwich Theorem Revisited Infinite Limits as x→a End Behavior Models Seeing Limits as x→±∞ ...
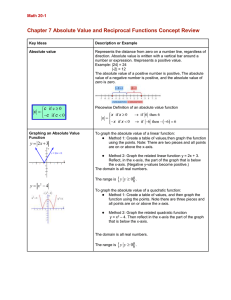
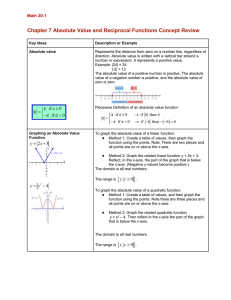
Chapter 7 Absolute Value and Reciprocal Functions Concept Review
... direction of opening (quadratic function) to determine which parts of the graph are above or below the xaxis. 3. Keep the parts that are positive (above x-axis) and indicate the domain. 4. Reflect the negative parts in the xaxis, multiply the expression by -1 for this part and indicate the domain. ...
... direction of opening (quadratic function) to determine which parts of the graph are above or below the xaxis. 3. Keep the parts that are positive (above x-axis) and indicate the domain. 4. Reflect the negative parts in the xaxis, multiply the expression by -1 for this part and indicate the domain. ...
Document
... algebraically, graphically, numerically in tables, or by verbal descriptions). Example: Given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change. Interpret the equation y = mx + b as ...
... algebraically, graphically, numerically in tables, or by verbal descriptions). Example: Given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change. Interpret the equation y = mx + b as ...
On the Existence of Triangles with Given Lengths of One Side and
... It is obvious that if a pair (x, y) satisfies (4), the pair (y, x) satisfies (5), and conversely. These equations therefore define inverse functions, and (5) defines a concave function (0, ∞) → (t, ∞) with an oblique asymptote y = x − a + 2t . Applying to functions y = y2 (x) and x = x1 (y) defined ...
... It is obvious that if a pair (x, y) satisfies (4), the pair (y, x) satisfies (5), and conversely. These equations therefore define inverse functions, and (5) defines a concave function (0, ∞) → (t, ∞) with an oblique asymptote y = x − a + 2t . Applying to functions y = y2 (x) and x = x1 (y) defined ...
Standard Graphs Worksheet
... End behavior: The disallowed values in the domain create vertical asymptotes….x = 0 is a vertical asymptote for this graph…the unattainable values in the range create horizontal asymptotes…y = 0 is a horizontal asymptote. Asymptotes are lines that shape the graph. Graphs cannot cross a vertical asym ...
... End behavior: The disallowed values in the domain create vertical asymptotes….x = 0 is a vertical asymptote for this graph…the unattainable values in the range create horizontal asymptotes…y = 0 is a horizontal asymptote. Asymptotes are lines that shape the graph. Graphs cannot cross a vertical asym ...
Asymptote
In analytic geometry, an asymptote (/ˈæsɪmptoʊt/) of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors. In some contexts, such as algebraic geometry, an asymptote is defined as a line which is tangent to a curve at infinity.The word asymptote is derived from the Greek ἀσύμπτωτος (asumptōtos) which means ""not falling together"", from ἀ priv. + σύν ""together"" + πτωτ-ός ""fallen"". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve.There are potentially three kinds of asymptotes: horizontal, vertical and oblique asymptotes. For curves given by the graph of a function y = ƒ(x), horizontal asymptotes are horizontal lines that the graph of the function approaches as x tends to +∞ or −∞. Vertical asymptotes are vertical lines near which the function grows without bound.More generally, one curve is a curvilinear asymptote of another (as opposed to a linear asymptote) if the distance between the two curves tends to zero as they tend to infinity, although the term asymptote by itself is usually reserved for linear asymptotes.Asymptotes convey information about the behavior of curves in the large, and determining the asymptotes of a function is an important step in sketching its graph. The study of asymptotes of functions, construed in a broad sense, forms a part of the subject of asymptotic analysis.