4 Polynomial and Rational Functions
... polynomial.”) Note that the degree is simply a whole number! Let us make special note of polynomials of degrees zero, one, and two. A polynomial of degree zero is something like f (x) = −2, which we also call a constant function. The term constant is used because the output f (x) remains the same (i ...
... polynomial.”) Note that the degree is simply a whole number! Let us make special note of polynomials of degrees zero, one, and two. A polynomial of degree zero is something like f (x) = −2, which we also call a constant function. The term constant is used because the output f (x) remains the same (i ...
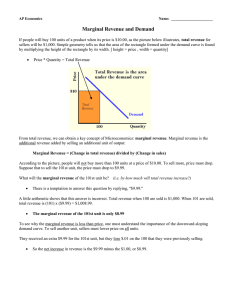
Why MR is below the Demand Curve
... additional revenue added by selling an additional unit of output: Marginal Revenue = (Change in total revenue) divided by (Change in sales) According to the picture, people will not buy more than 100 units at a price of $10.00. To sell more, price must drop. Suppose that to sell the 101st unit, the ...
... additional revenue added by selling an additional unit of output: Marginal Revenue = (Change in total revenue) divided by (Change in sales) According to the picture, people will not buy more than 100 units at a price of $10.00. To sell more, price must drop. Suppose that to sell the 101st unit, the ...
Thinking Mathematically by Robert Blitzer
... sharp corners. By Smooth rounded rounded corner corner continuous, we mean that the graph has no breaks and can be drawn without lifting x x your pencil from the rectangular coordinate system. These ideas are Smooth Smooth rounded rounded illustrated in the figure. corner corner ...
... sharp corners. By Smooth rounded rounded corner corner continuous, we mean that the graph has no breaks and can be drawn without lifting x x your pencil from the rectangular coordinate system. These ideas are Smooth Smooth rounded rounded illustrated in the figure. corner corner ...
Trigonometry Scrapbook
... Page 1- Parallel Lines Page 2- Two Congruent Objects Page 3- Vertical Angles Page4- Perpendicular Lines Page 5- Sine Page 6-Cosine Page 7- Tangent Page 8-Adjacent Page9- Similarity Page 10- Secant Page 11-Amplitude Page 12- Cotangent Page 13- Diameter Page 14- Cosecant Page 15- Period ...
... Page 1- Parallel Lines Page 2- Two Congruent Objects Page 3- Vertical Angles Page4- Perpendicular Lines Page 5- Sine Page 6-Cosine Page 7- Tangent Page 8-Adjacent Page9- Similarity Page 10- Secant Page 11-Amplitude Page 12- Cotangent Page 13- Diameter Page 14- Cosecant Page 15- Period ...
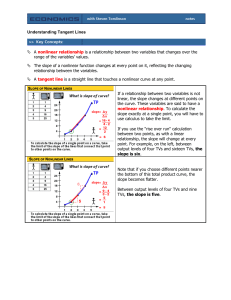
Understanding Tangent Lines A nonlinear relationship is a
... A nonlinear relationship is a relationship between two variables that changes over the range of the variables' values. The slope of a nonlinear function changes at every point on it, reflecting the changing relationship between the variables. A tangent line is a straight line that touches a nonlinea ...
... A nonlinear relationship is a relationship between two variables that changes over the range of the variables' values. The slope of a nonlinear function changes at every point on it, reflecting the changing relationship between the variables. A tangent line is a straight line that touches a nonlinea ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 16. Find the locus of poles of chords of the parabola which subtend a right angle at the vertex. 17. Prove that any two straight lines through the points of intersection of an ellipse with any circle make equal angles with the axes of the ellipse. 18. Show that the asymptotes of a rectangular hyperb ...
... 16. Find the locus of poles of chords of the parabola which subtend a right angle at the vertex. 17. Prove that any two straight lines through the points of intersection of an ellipse with any circle make equal angles with the axes of the ellipse. 18. Show that the asymptotes of a rectangular hyperb ...
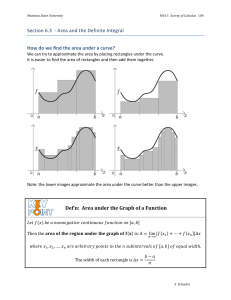
Section 6.3 -‐ Area and the Definite Integral How do we find the a
... Using Rectangles to Approximate Area under a Curve ...
... Using Rectangles to Approximate Area under a Curve ...
here - UBC Math
... algebraically, or determine the limit does not exist and explain why it does not exist; if the limit is of the form 0/0, use algebraic manipulations (e.g. factoring) to evaluate it. c) Give examples of rational functions whose limits at a given finite number of points do not exist. d) Evaluate limit ...
... algebraically, or determine the limit does not exist and explain why it does not exist; if the limit is of the form 0/0, use algebraic manipulations (e.g. factoring) to evaluate it. c) Give examples of rational functions whose limits at a given finite number of points do not exist. d) Evaluate limit ...
Mr. Benson BC Calculus Midterm Practice Problems Answers Solve
... Find the vertical asymptotes of the graph of f(x). ...
... Find the vertical asymptotes of the graph of f(x). ...
DAB α - KSAintern
... On the boat to Denmark, a travel agency displays brochures for a bus tour. From previous experience it is known that 65% of the passengers read the brochure. 30% of the readers book the bus tour spontaneously, the rest of the readers will book the bus tour with a probability of 40% later. Find the p ...
... On the boat to Denmark, a travel agency displays brochures for a bus tour. From previous experience it is known that 65% of the passengers read the brochure. 30% of the readers book the bus tour spontaneously, the rest of the readers will book the bus tour with a probability of 40% later. Find the p ...
lecture 2
... In many applications the tool is a ball-end cutter. For a two-axis machine. cutting in a specified plane the ball-end cutter can be considered a circular disk of fixed radius d. Suppose the shape to be cut is the trace of a regular curve C(t) = (x(t), y(t)), with unit normal n(t). Referring to Figu ...
... In many applications the tool is a ball-end cutter. For a two-axis machine. cutting in a specified plane the ball-end cutter can be considered a circular disk of fixed radius d. Suppose the shape to be cut is the trace of a regular curve C(t) = (x(t), y(t)), with unit normal n(t). Referring to Figu ...
Math Test Study Guide (MPT)
... 10. Interpret the meaning of intercept and slope of a linear function in a given context; 11. Given a point (x1, y1) and the slope m, find the equation of a line 12. Given the equations of two lines, determine if they are parallel, perpendicular or neither 13. Solve a formula for a specified variabl ...
... 10. Interpret the meaning of intercept and slope of a linear function in a given context; 11. Given a point (x1, y1) and the slope m, find the equation of a line 12. Given the equations of two lines, determine if they are parallel, perpendicular or neither 13. Solve a formula for a specified variabl ...
Asymptote
In analytic geometry, an asymptote (/ˈæsɪmptoʊt/) of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors. In some contexts, such as algebraic geometry, an asymptote is defined as a line which is tangent to a curve at infinity.The word asymptote is derived from the Greek ἀσύμπτωτος (asumptōtos) which means ""not falling together"", from ἀ priv. + σύν ""together"" + πτωτ-ός ""fallen"". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve.There are potentially three kinds of asymptotes: horizontal, vertical and oblique asymptotes. For curves given by the graph of a function y = ƒ(x), horizontal asymptotes are horizontal lines that the graph of the function approaches as x tends to +∞ or −∞. Vertical asymptotes are vertical lines near which the function grows without bound.More generally, one curve is a curvilinear asymptote of another (as opposed to a linear asymptote) if the distance between the two curves tends to zero as they tend to infinity, although the term asymptote by itself is usually reserved for linear asymptotes.Asymptotes convey information about the behavior of curves in the large, and determining the asymptotes of a function is an important step in sketching its graph. The study of asymptotes of functions, construed in a broad sense, forms a part of the subject of asymptotic analysis.