Download f(x)

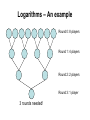
Math Tutorial
Lecture 2
Some of these slides are courtesy of D. Plaisted, UNC and M. Nicolescu, UNR
Exponentials – What are they?
• Simply: a number (base) raised to a power
(exponent).
Exponentials – A quick explanation
• Simply: a number (base) raised to a power
(exponent).
• Easy enough to calculate:
b
•
•
•
•
ab = a × a × a … × a
So there are ‘b’ lots of ‘a’
What is 43?
4 × 4 × 4 = 64
Exponentials in Computer Science
• Have you ever noticed the following numbers
popping up in your computer science studies?
• 1, 2, 4, 8, 16, 32, 64, 128…1024…
• What do they all have in common?
• They are all powers of 2!!
Exponentials in Computer Science
• The powers of 2 should be (very) familiar to you
by now.
• All the computers you have been using work in
binary bits (at the lowest level)…
• 2 values: 0/1, true/false etc
• all ‘data sizes’ must be expressed in powers of
2.
Exponentials in Computer Science
•
•
•
•
•
•
•
1 kilobyte ≠ 1000 bytes (‘standard’ use of kilo)
1 kilobyte = 1024 bytes
Because…
29 = 512
210 = 1024
211 = 2048
So 210 is the closest we can get to 1000
Working with Exponentials
• First, some easy exponentials to
remember:
• a0 = 1
• a1 = a
Exponentials
• Useful Identities:
1
a 
a
(a m ) n  a mn
1
a m a n  a m n
Logarithms
• This is because log(arithm)s are just ‘reversed’
exponentials
• E.g. if 24 = 16
• log216 = 4
– base is 2
• Logarithms ‘map’ large numbers onto smaller
numbers
Logarithms - Bases
• There are several common bases:
– 10: very common base, Richter scale etc.
– e: used by a lot of scientists
– 2: very common in computer science. WHY?
Logarithms – An example
• Imagine US open: 8 players left.
• It is a knockout tournament, so every time that 2 players
play the losing player is eliminated from the tournament
and the winning plays goes on to the next round.
• How many rounds must be played to determine an
overall winner?
Logarithms – An example
• Imagine US open: 8 players left.
• It is a knockout tournament, so every time that 2 players
play the losing player is eliminated from the tournament
and the winning plays goes on to the next round.
• How many rounds must be played to determine an
overall winner?
• What stage: semi-final? quarterfinal? 1/8? 1/16?
Logarithms – An example
Round 0: 8 players
Round 1: 4 players
Round 2: 2 players
Round 3: 1 player
3 rounds needed!
Logarithms – Example explained
• 3 rounds are needed to determine the winner of 8 teams,
competing 2 at a time (i.e. one-on-one)
• This can be easily calculated using logs.
• 2 teams play at a time, so the base is 2. (i.e. 2x = 8, so
we need to use log2)
• So, log2 8 = ….
• 3
Logarithms
• In algorithm analysis we often use the notation
“log n” without specifying the base
Binary logarithm
lg n  log 2 n
Natural logarithm
ln n  log e n
log k n  (log n )k
log log n  log(log n )
log x y  y log x
log xy  log x  log y
x
log  log x  log y
y
log a x  log a b log b x
a logb x 
x logb a
Logarithms and exponentials –
Bases
• If the base of a logarithm is changed from one constant to
another, the value is altered by a constant factor.
– Ex: log10 n * log210 = log2 n.
– Base of logarithm is not an issue in asymptotic notation.
• Exponentials with different bases differ by a exponential
factor (not a constant factor).
– Ex: 2n = (2/3)n*3n.
Some Simple Summation Formulas
• Arithmetic series:
n
 k  1  2  ...  n 
k 1
• Geometric series:
– Special case: x < 1:
x n 1  1
x  1  x  x  ...  x 
x  1

x 1
k 0
n
k

x
k 0
• Harmonic series:
n ( n  1)
2
k
2

n
1
1 x
n
1
1
1
 ln n

1


...


k
2
n
k 1
n
• Other important formulas: 
lg k  n lg n
k 1
n
 k p  1p  2 p  ...  n p 
k 1
1
n p 1
p 1
Limit
• Def (informal): a limit is the intended height of a function
f(x)
g(x)
4
3
x
x
Parabola
•
•
Different x values have different height (f(x) value)
Function changes its height for x within the x domain
f(x) = x2
f(1) = 1
f(2) = 4
f(x)
f ( x)  4
lim x 2
When x is getting close to the value of 2
the function f(x) getting close to 4
Limit: Formal Definition
f(x)
x2  6x  8
f ( x) 
x2
22  6 * 2  8 0
f (2) 

22
0
lim f ( x)  2
2
-2
x
x 2
f(2) is not defined but limit for f(2) exists
Karl Weierstrass formally defined a limit as follows (epsilon-delta definition):
Let f be a real-valued function defined on an open interval of real numbers
containing c (except possibly at c) and let L be a real number. Then
lim f ( x)  L
x c
means that
for each real ε > 0 there exists a real δ > 0 such that for all x with
0 < |x − c| < δ, we have |f(x) − L| < ε.
xc
c
Whenever a point x is within δ units of c, f(x) is within ε units of L
When does a Limit Exist?
f(x)
2
x
lim f ( x)  3
Right-hand limit
(limit from above)
x 2
Left-hand limit
(limit from below)
lim f ( x)  1.5
x 2
lim f ( x)exists  if lim f ( x)  lim f ( x)
x 2
x 2
x2
f(x)
Limit does not exist for x=2, but
exists for other x’s (for example,
for x=1)
2
x
f(x)
2
x
Limit exists for x=2 even if f(x) is
not defined for x=2
How to Find/Evaluate a Limit. 1
• Substitution
x 1
f ( x) 
2x  3
2
0 1
1
lim f ( x) 

x 0
2*0  3
3
2
How to Find/Evaluate a Limit. 2
• Factoring
x  6 x  8 ( x  4)( x  2)
f ( x) 

 x4
x2
x2
lim f ( x)  2  4  2
2
x 2
How to Find/Evaluate a Limit. 3
• Conjugate method
x 4
x  16
lim f ( x)  ?
f ( x) 
x 16
x 4
x 4
x  16
f ( x) 
*

x  16
x  4 ( x  16) * ( x  4)
1
1
lim f ( x)  lim

x 16
x 16
x 4 8
Limits and Infinity (lim and ∞)
Non-zero number divided by
0  vertical asymptote
Asymptote cannot be reached
lim  f ( x)  
x 4
lim f ( x)  
x 4 
Limits and Infinity (lim and ∞)
Non-zero number divided by
0  vertical asymptote
Asymptote cannot be reached
lim  f ( x)  
x 4
lim f ( x)  
x 4 
x=-4 is a vertical asymptote
Limits and Infinity (lim and ∞)
y=3 is a horizontal asymptote
lim f ( x)  3
x 
lim f ( x)  3
x 
Limit at ∞
• x is getting infinitely large  limit at ∞
• To calculate a limit at infinity, compare the degrees in the top and
bottom of the fraction (in general case, the top and the bottom of
the fraction)
a( x)
f ( x) 
b( x )
4 x3  4 x 2  5
f ( x) 
6x2  7x  2
2 x3  4 x 2  5
f ( x)  5
6 x  7 x3  x  2
4 x 3  3x 2  5
f ( x) 
7 x3  7 x  2
Compare the degree of the
nominator a(x) and the degree
of the denominator b(x)
Degree a(x) > degree b(x) 
There is no horizontal asymptote
Degree a(x) < degree b(x) 
Horizontal asymptote: y=0
Degree a(x) = degree b(x).
The ratio of the coefficiencies
of the highest terms
lim f ( x )  
x 
lim f ( x )  0
x 
4
lim f ( x ) 
x 
7
Limit and ∞
• Limit equals ∞  function increases infinitely (∞ is not
number)
• Vertical asymptote
• Horizontal asymptote
• L’Hopital’s Rule
Monotonicity
• f(n) is
–
–
–
–
monotonically increasing if m  n  f(m)  f(n).
monotonically decreasing if m  n  f(m)  f(n).
strictly increasing if m < n  f(m) < f(n).
strictly decreasing if m > n  f(m) > f(n).
32
Exponentials
• Useful Identities:
1
a 
a
(a m ) n  a mn
1
a m a n  a m n
• Exponentials and polynomials
nb
lim n  0
n a
 n b  o( a n )
33