12.1: What are electromagnetic waves?
... We define a wave as a disturbance that carries energy and a particle as a piece of matter. EM waves can behave as both a wave and a particle (the particle-wave duality). Phenomenon discovered in 1887 by Heinrich Hertz. Experiment known as the “photo-electric effect”: Shine a light on metal and ...
... We define a wave as a disturbance that carries energy and a particle as a piece of matter. EM waves can behave as both a wave and a particle (the particle-wave duality). Phenomenon discovered in 1887 by Heinrich Hertz. Experiment known as the “photo-electric effect”: Shine a light on metal and ...
Chapter 5 Worksheet 1
... 1. State Heisenberg’s Uncertainty Principle as it pertains to atomic theory. It is impossible to determine the exact location and momentum of a moving object at the same time. 2. Why does the observation of a very small object such as an electron cause the electron to have its motion changed? The po ...
... 1. State Heisenberg’s Uncertainty Principle as it pertains to atomic theory. It is impossible to determine the exact location and momentum of a moving object at the same time. 2. Why does the observation of a very small object such as an electron cause the electron to have its motion changed? The po ...
Slide 1
... phenomenon and not matter Max Planck developed a new physics when classical physics could not be used to interpret data from blackbody radiation ( Blackbody is an object that absorbs all radiation incident on it) Blackbody radiation is emitted by solid bodies that are heated to high T and become inc ...
... phenomenon and not matter Max Planck developed a new physics when classical physics could not be used to interpret data from blackbody radiation ( Blackbody is an object that absorbs all radiation incident on it) Blackbody radiation is emitted by solid bodies that are heated to high T and become inc ...
The Zeeman Effect
... The same expressions, but with ml and ms replaced by ML and MS, apply to the combined magnetic moments of several coupled electrons. When an atom has L≠0 and S≠0, these net magnetic moments are simply additive. Spin-orbit coupling (itself a magnetic effect) is usually large enough that the total ele ...
... The same expressions, but with ml and ms replaced by ML and MS, apply to the combined magnetic moments of several coupled electrons. When an atom has L≠0 and S≠0, these net magnetic moments are simply additive. Spin-orbit coupling (itself a magnetic effect) is usually large enough that the total ele ...
Electromagnetic Spectrum activity
... The letter describing the sub-level is preceded by the value of n for the energy level e.g. 3d, 4f, 2p. Each sublevel contains orbitals (space occupied by a pair of electrons). The third quantum number, ml (magnetic quantum number) is used to describe each orbital within in a sublevel. There are 3 o ...
... The letter describing the sub-level is preceded by the value of n for the energy level e.g. 3d, 4f, 2p. Each sublevel contains orbitals (space occupied by a pair of electrons). The third quantum number, ml (magnetic quantum number) is used to describe each orbital within in a sublevel. There are 3 o ...
6. Quantum Mechanics II
... which is a sine wave moving in the x direction. Notice that, unlike classical waves, we are not taking the real part of this function. is, in fact, complex. In general, the wave function is complex. But the physically measurable quantities must be real. These include the probability, position, mom ...
... which is a sine wave moving in the x direction. Notice that, unlike classical waves, we are not taking the real part of this function. is, in fact, complex. In general, the wave function is complex. But the physically measurable quantities must be real. These include the probability, position, mom ...
lect22
... variables” which we do not know but which gives the system an underlying deterministic structure. We hide our ignorance by describing the “most probable” outcomes of measurement ...
... variables” which we do not know but which gives the system an underlying deterministic structure. We hide our ignorance by describing the “most probable” outcomes of measurement ...
Dispersion of electromagnetic waves in simple dielectrics “Dispersion” means that optical
... m x’’ = −k x − γ x’ − e E0 exp{ -i ωt } The STEADY STATE SOLUTION is x(t) = x0 exp{ -i ωt } ; i.e., the electron oscillates at the driving frequency ω. The only question is, what is the amplitude of oscillation? (k − m ω2 − i ω γ )x0 = − e E0 x0 = ...
... m x’’ = −k x − γ x’ − e E0 exp{ -i ωt } The STEADY STATE SOLUTION is x(t) = x0 exp{ -i ωt } ; i.e., the electron oscillates at the driving frequency ω. The only question is, what is the amplitude of oscillation? (k − m ω2 − i ω γ )x0 = − e E0 x0 = ...
Problem set 9
... 3. Calculate h x̂i at time t in the above gaussian wave packet. Since ψ̃(k, t) is known, it is good to work in the momentum basis. So you need to know how x̂ acts in k -space. This was worked ...
... 3. Calculate h x̂i at time t in the above gaussian wave packet. Since ψ̃(k, t) is known, it is good to work in the momentum basis. So you need to know how x̂ acts in k -space. This was worked ...
WAVE MECHANICS (Schrödinger, 1926)
... mechanics which takes into account the wave nature of matter and the uncertainty principle. * The state of an electron is described by a function y, called the “wave function”. * y can be obtained by solving Schrödinger’s equation (a differential equation): Hy=Ey ...
... mechanics which takes into account the wave nature of matter and the uncertainty principle. * The state of an electron is described by a function y, called the “wave function”. * y can be obtained by solving Schrödinger’s equation (a differential equation): Hy=Ey ...
Ch. 4: Electron Configuration
... Mullis Chemistry Holt Ch.4 allowed orbits with a fixed energy. ...
... Mullis Chemistry Holt Ch.4 allowed orbits with a fixed energy. ...
Homework 4 Answer Key
... For the n = 0 level, the total energy is zero (stationary disk). This is the lowest level and it is not degenerate. The next higher level has energy h 2 , but this can be achieved for either n = 1 or n = –1 (the disk has ! the same kinetic energy whether it is rotating clockwise or counterclockwise) ...
... For the n = 0 level, the total energy is zero (stationary disk). This is the lowest level and it is not degenerate. The next higher level has energy h 2 , but this can be achieved for either n = 1 or n = –1 (the disk has ! the same kinetic energy whether it is rotating clockwise or counterclockwise) ...
Models of the Atom
... Could not explain why emission lines are double, triple or more Could not explain why some lines brighter than others Could not explain how atoms bond Mixed classical and quantum ideas ...
... Could not explain why emission lines are double, triple or more Could not explain why some lines brighter than others Could not explain how atoms bond Mixed classical and quantum ideas ...
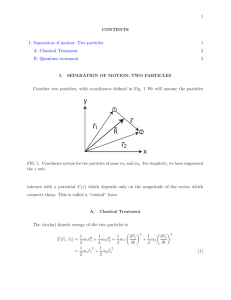
Separation of internal and center-of
... where µ ≡ m1 m2 /(m1 + m2 ) is the “reduced” mass. Thus, since the potential depends only on |~r|, the Hamiltonian separates into a term describing the kinetic energy of the center-of-mass, moving through space with mass M, and the kinetic energy and potential energy of the relative motion of partic ...
... where µ ≡ m1 m2 /(m1 + m2 ) is the “reduced” mass. Thus, since the potential depends only on |~r|, the Hamiltonian separates into a term describing the kinetic energy of the center-of-mass, moving through space with mass M, and the kinetic energy and potential energy of the relative motion of partic ...
30-32: Main Topics
... electron shell theories • electrons in stable ‘orbits’ • collisions cause electron “planets” to move to larger, higher energy, orbits • “light” energy emitted when they drop back to their original smaller orbits ...
... electron shell theories • electrons in stable ‘orbits’ • collisions cause electron “planets” to move to larger, higher energy, orbits • “light” energy emitted when they drop back to their original smaller orbits ...
CHM1045 - Michael Blaber
... * = c (the relationship between wavelength, frequency and speed of light for electromagnetic radiation) E = h * (the relationship between energy and frequency for electromagnetic radiation En = -RH / n2 or En = -B / n2 (the relationship between the energy of an electron in Bohr's model of the ...
... * = c (the relationship between wavelength, frequency and speed of light for electromagnetic radiation) E = h * (the relationship between energy and frequency for electromagnetic radiation En = -RH / n2 or En = -B / n2 (the relationship between the energy of an electron in Bohr's model of the ...
uncertainty, atom
... 1) An orbiting electron is an accelerating charge, and accelerating charges give off EM radiation (like an antenna), thus giving off energy. The electron would gradually lose all its energy. That doesn’t happen -- atoms are stable. ...
... 1) An orbiting electron is an accelerating charge, and accelerating charges give off EM radiation (like an antenna), thus giving off energy. The electron would gradually lose all its energy. That doesn’t happen -- atoms are stable. ...
CHAPTER 5
... 2. An electron may move from one discrete energy level (orbit) to another, but to do so energy is emitted or absorbed 3. An electron moves in a spherical orbit around the nucleus -If e- are in quantized energy states, then ∆E of states can have only certain values -This explains sharp line spectra ( ...
... 2. An electron may move from one discrete energy level (orbit) to another, but to do so energy is emitted or absorbed 3. An electron moves in a spherical orbit around the nucleus -If e- are in quantized energy states, then ∆E of states can have only certain values -This explains sharp line spectra ( ...
Riemannian method in quantum field theory about curved space-time
... Starting from a given Lorentz metric g~k on a space-time manifold M and a tube T of world lines along which observers may move, we describe an algorithm to obtain the quantum theory of scalar particles of mass m. Let ei denote the 4-velocities of the world lines, and let V~, s real, be a family o f ...
... Starting from a given Lorentz metric g~k on a space-time manifold M and a tube T of world lines along which observers may move, we describe an algorithm to obtain the quantum theory of scalar particles of mass m. Let ei denote the 4-velocities of the world lines, and let V~, s real, be a family o f ...
Chapter 3
... theory. Describe their model and explain limitations. o Dalton’s Billiard Ball Model o Thomson’s Raisin Bun Model o Rutherford’s Nuclear Model o Bohr’s Planetary Model b. Explain Rutherford’s gold foil experiment and it’s significance c. Explain atomic spectra and it’s significance to Bohr’s model 2 ...
... theory. Describe their model and explain limitations. o Dalton’s Billiard Ball Model o Thomson’s Raisin Bun Model o Rutherford’s Nuclear Model o Bohr’s Planetary Model b. Explain Rutherford’s gold foil experiment and it’s significance c. Explain atomic spectra and it’s significance to Bohr’s model 2 ...
Quantum Theory 1 - Home Exercise 4
... 4. Particle on a ring - Consider a particle that is free to move on a ring of circumference L, such that ψ(x, t) = ψ(x + L, t) (a) Find the normalized stationary states of the system and explicitly show that they form an orthonormal basis. (b) Calculate the dispersion relation ωn (kn ) and show that ...
... 4. Particle on a ring - Consider a particle that is free to move on a ring of circumference L, such that ψ(x, t) = ψ(x + L, t) (a) Find the normalized stationary states of the system and explicitly show that they form an orthonormal basis. (b) Calculate the dispersion relation ωn (kn ) and show that ...
Queens College Department of Physics - Qc.edu
... modern physics laws often contradict your common sense, they correctly describe and predict the results of the experiments on sub-atomic scale. You will get perspective on how parallel and independent discoveries converge to give new and advanced knowledge, and how these discoveries not only provide ...
... modern physics laws often contradict your common sense, they correctly describe and predict the results of the experiments on sub-atomic scale. You will get perspective on how parallel and independent discoveries converge to give new and advanced knowledge, and how these discoveries not only provide ...
Wave-particle_duality
... An α-particle having a de Broglie wavelength λi collides with a stationary carbon nucleus. The α-particle moves off in a different direction as shown below. final direction of –particle, de Broglie wavelength f ...
... An α-particle having a de Broglie wavelength λi collides with a stationary carbon nucleus. The α-particle moves off in a different direction as shown below. final direction of –particle, de Broglie wavelength f ...