Derivation of the Pauli exchange principle
... where x is a set of space coordinates, and s represents a set of spin quantum numbers. Pauli [1] showed that this relation connecting fermion and boson statistics with spin can be derived with the aid of relativistic quantum field theory. As will be seen below, it can also be derived directly from t ...
... where x is a set of space coordinates, and s represents a set of spin quantum numbers. Pauli [1] showed that this relation connecting fermion and boson statistics with spin can be derived with the aid of relativistic quantum field theory. As will be seen below, it can also be derived directly from t ...
Particle-like Properties of Electromagnetic Radiation
... function or orbital - solution to the wave equation. 1) has a specific energy 2) contains information about the an electron s position (or probability) in 3D space. 3) gives the probability of finding an electron within a given region 4) defines a volume of space around the nucleus where there is a ...
... function or orbital - solution to the wave equation. 1) has a specific energy 2) contains information about the an electron s position (or probability) in 3D space. 3) gives the probability of finding an electron within a given region 4) defines a volume of space around the nucleus where there is a ...
Quantum Problems 1. Consider a quantum system whose state at
... then H1 |ψn i is the zero vector. In this problem, as is standard, we have chosen the first-order ...
... then H1 |ψn i is the zero vector. In this problem, as is standard, we have chosen the first-order ...
The Particulate Nature of Light
... - e.g., the deflection of a stream of electrons is just like the path of a projectile. Electrons can also exhibit wave properties - e.g., they can demonstrate diffraction. De Broglie proposed that an electron of mass m moving with speed v would have a wavelength given by: = h/p This equation gives ...
... - e.g., the deflection of a stream of electrons is just like the path of a projectile. Electrons can also exhibit wave properties - e.g., they can demonstrate diffraction. De Broglie proposed that an electron of mass m moving with speed v would have a wavelength given by: = h/p This equation gives ...
E489: Decay of a particle with spin 0
... Solving eqs.(8) is difficult, because it would require us to compute the transition matrix, using the operators Jx , Jy which ”live” in the full Hilbert space, whose dimension is given in eq.(4). However, it is easy to see from eqs.(8) that the coefficients depend only on 2 free parameters, the same ...
... Solving eqs.(8) is difficult, because it would require us to compute the transition matrix, using the operators Jx , Jy which ”live” in the full Hilbert space, whose dimension is given in eq.(4). However, it is easy to see from eqs.(8) that the coefficients depend only on 2 free parameters, the same ...
Quantum Physics - The University of Sydney
... There is no easy road to learning. Your marks will depend on the work that you do. You should read through and understand the sections of the textbook specified below, and work through the specified examples. You should attempt as many as possible of the recommended Questions, Exercises and Problems ...
... There is no easy road to learning. Your marks will depend on the work that you do. You should read through and understand the sections of the textbook specified below, and work through the specified examples. You should attempt as many as possible of the recommended Questions, Exercises and Problems ...
Professor Jason Twamley
... Simulating higher transcendental mathematical functions with quantum mechanics J. Twamley and G.J. Milburn Quantum Information Science, Centre for Quantum Computer Technology Physics Department, Division of Information and Communication Sciences Macquarie University, NSW 2109 Australia Tel: +61-2-98 ...
... Simulating higher transcendental mathematical functions with quantum mechanics J. Twamley and G.J. Milburn Quantum Information Science, Centre for Quantum Computer Technology Physics Department, Division of Information and Communication Sciences Macquarie University, NSW 2109 Australia Tel: +61-2-98 ...
Quantum Mechanics
... Electron orbitals • The shape of the electron orbitals is given by the solution to the Schrodinger equation ...
... Electron orbitals • The shape of the electron orbitals is given by the solution to the Schrodinger equation ...
Homework 3 - barnes report
... under “Normal distribution” or “Error function” for the numerical value of the integral. ...
... under “Normal distribution” or “Error function” for the numerical value of the integral. ...
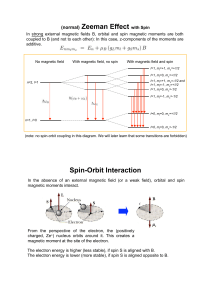
(normal) Zeeman Effect with Spin Spin
... magnetic moment at the site of the electron. The electron energy is higher (less stable), if spin S is aligned with B. The electron energy is lower (more stable), if spin S is aligned opposite to B. ...
... magnetic moment at the site of the electron. The electron energy is higher (less stable), if spin S is aligned with B. The electron energy is lower (more stable), if spin S is aligned opposite to B. ...
Wave function

A wave function in quantum mechanics describes the quantum state of an isolated system of one or more particles. There is one wave function containing all the information about the entire system, not a separate wave function for each particle in the system. Its interpretation is that of a probability amplitude. Quantities associated with measurements, such as the average momentum of a particle, can be derived from the wave function. It is a central entity in quantum mechanics and is important in all modern theories, like quantum field theory incorporating quantum mechanics, while its interpretation may differ. The most common symbols for a wave function are the Greek letters ψ or Ψ (lower-case and capital psi).For a given system, once a representation corresponding to a maximal set of commuting observables and a suitable coordinate system is chosen, the wave function is a complex-valued function of the system's degrees of freedom corresponding to the chosen representation and coordinate system, continuous as well as discrete. Such a set of observables, by a postulate of quantum mechanics, are Hermitian linear operators on the space of states representing a set of physical observables, like position, momentum and spin that can, in principle, be simultaneously measured with arbitrary precision. Wave functions can be added together and multiplied by complex numbers to form new wave functions, and hence are elements of a vector space. This is the superposition principle of quantum mechanics. This vector space is endowed with an inner product such that it is a complete metric topological space with respect to the metric induced by the inner product. In this way the set of wave functions for a system form a function space that is a Hilbert space. The inner product is a measure of the overlap between physical states and is used in the foundational probabilistic interpretation of quantum mechanics, the Born rule, relating transition probabilities to inner products. The actual space depends on the system's degrees of freedom (hence on the chosen representation and coordinate system) and the exact form of the Hamiltonian entering the equation governing the dynamical behavior. In the non-relativistic case, disregarding spin, this is the Schrödinger equation.The Schrödinger equation determines the allowed wave functions for the system and how they evolve over time. A wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name ""wave function"", and gives rise to wave–particle duality. The wave of the wave function, however, is not a wave in physical space; it is a wave in an abstract mathematical ""space"", and in this respect it differs fundamentally from water waves or waves on a string.For a given system, the choice of which relevant degrees of freedom to use are not unique, and correspondingly the domain of the wave function is not unique. It may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space, the two are related by a Fourier transform. These descriptions are the most important, but they are not the only possibilities. Just like in classical mechanics, canonical transformations may be used in the description of a quantum system. Some particles, like electrons and photons, have nonzero spin, and the wave function must include this fundamental property as an intrinsic discrete degree of freedom. In general, for a particle with half-integer spin the wave function is a spinor, for a particle with integer spin the wave function is a tensor. Particles with spin zero are called scalar particles, those with spin 1 vector particles, and more generally for higher integer spin, tensor particles. The terminology derives from how the wave functions transform under a rotation of the coordinate system. No elementary particle with spin 3⁄2 or higher is known, except for the hypothesized spin 2 graviton. Other discrete variables can be included, such as isospin. When a system has internal degrees of freedom, the wave function at each point in the continuous degrees of freedom (e.g. a point in space) assigns a complex number for each possible value of the discrete degrees of freedom (e.g. z-component of spin). These values are often displayed in a column matrix (e.g. a 2 × 1 column vector for a non-relativistic electron with spin 1⁄2).In the Copenhagen interpretation, an interpretation of quantum mechanics, the squared modulus of the wave function, |ψ|2, is a real number interpreted as the probability density of measuring a particle as being at a given place at a given time or having a definite momentum, and possibly having definite values for discrete degrees of freedom. The integral of this quantity, over all the system's degrees of freedom, must be 1 in accordance with the probability interpretation, this general requirement a wave function must satisfy is called the normalization condition. Since the wave function is complex valued, only its relative phase and relative magnitude can be measured. Its value does not in isolation tell anything about the magnitudes or directions of measurable observables; one has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.The unit of measurement for ψ depends on the system, and can be found by dimensional analysis of the normalization condition for the system. For one particle in three dimensions, its units are [length]−3/2, because an integral of |ψ|2 over a region of three-dimensional space is a dimensionless probability.