Meadowlands SHAPES
... Moving on to triangles and looking at calculating the area of them. All angles add up to 180. WORKSHEET 2 – FINDING AREA BY COUNTING SQUARES. Areas of triangles – there is a formula but first we’ll look at how we get to it. Take a rectangle and cut it in half – 2 triangles. These triangles should be ...
... Moving on to triangles and looking at calculating the area of them. All angles add up to 180. WORKSHEET 2 – FINDING AREA BY COUNTING SQUARES. Areas of triangles – there is a formula but first we’ll look at how we get to it. Take a rectangle and cut it in half – 2 triangles. These triangles should be ...
Homework
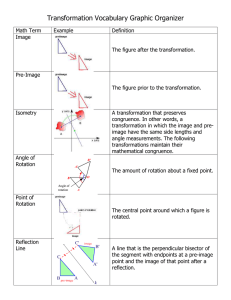
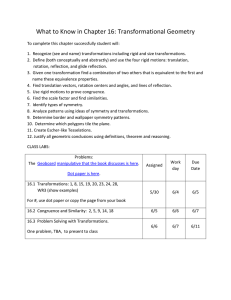
... What to Know in Chapter 16: Transformational Geometry To complete this chapter successfully student will: 1. Recognize (see and name) transformations including rigid and size transformations. 2. Define (both conceptually and abstractly) and use the four rigid motions: translation, rotation, reflecti ...
... What to Know in Chapter 16: Transformational Geometry To complete this chapter successfully student will: 1. Recognize (see and name) transformations including rigid and size transformations. 2. Define (both conceptually and abstractly) and use the four rigid motions: translation, rotation, reflecti ...