Important things to remember for the Geometry EOC
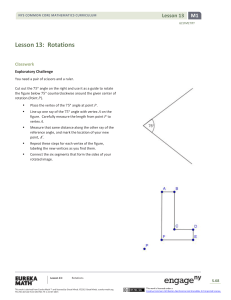
... b. Inverse: “SAY NO” c. Contrapositive: “FLIP AND SAY NO” d. COUNTEREXAMPLE: Example that proves something is FALSE. 2. Biconditionals: “… , if and only if …” a. ONLY IF CONDITIONAL AND CONVERSE ARE BOTH TRUE! 3. Translations: “SLIDE” a. (x,y) (x ...
... b. Inverse: “SAY NO” c. Contrapositive: “FLIP AND SAY NO” d. COUNTEREXAMPLE: Example that proves something is FALSE. 2. Biconditionals: “… , if and only if …” a. ONLY IF CONDITIONAL AND CONVERSE ARE BOTH TRUE! 3. Translations: “SLIDE” a. (x,y) (x ...
0 1 0 0 0 0 1 0 0 0 0 1
... • Several different ways of deriving the specific formulas for arbitrary rotation in 3D space: – a) The method presented here . (See pgs 266-269) – b) The use of the vector dot product to establish the sin of angle and the use of the vector cross product to determine the cosin of the angle. (See pgs ...
... • Several different ways of deriving the specific formulas for arbitrary rotation in 3D space: – a) The method presented here . (See pgs 266-269) – b) The use of the vector dot product to establish the sin of angle and the use of the vector cross product to determine the cosin of the angle. (See pgs ...