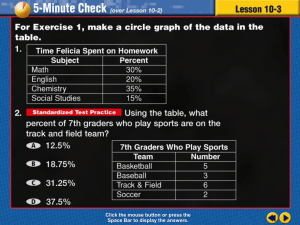
Answer - Skyline School
... The variable (mRQS) is being added by 560 Do the inverse on both sides of the equal sign Bring down 560 ...
... The variable (mRQS) is being added by 560 Do the inverse on both sides of the equal sign Bring down 560 ...
Conjectures for Geometry for Math 70 By I. L. Tse Chapter 2
... 1. Triangle Sum Conjecture – the sum of the measures of angles in every triangle is 180°. 2. Isosceles Triangle Conjecture: If a triangle is isosceles, then its base angles are congruent. 3. Converse of the Isosceles Triangle Conjecture: If a triangle has two congruent angles, then the triangle is ...
... 1. Triangle Sum Conjecture – the sum of the measures of angles in every triangle is 180°. 2. Isosceles Triangle Conjecture: If a triangle is isosceles, then its base angles are congruent. 3. Converse of the Isosceles Triangle Conjecture: If a triangle has two congruent angles, then the triangle is ...