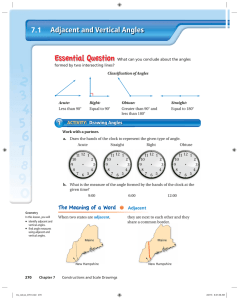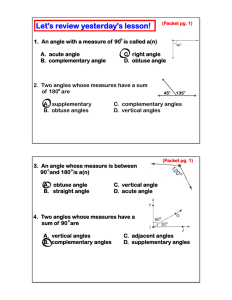
Angles and Angle Measure
... A line that intersects two (or more) parallel lines is called a transversal. The transversal and the parallel lines form a total of eight angles. There are many pairs of congruent angles and many pairs of supplementary angles. ...
... A line that intersects two (or more) parallel lines is called a transversal. The transversal and the parallel lines form a total of eight angles. There are many pairs of congruent angles and many pairs of supplementary angles. ...
DRAFT Errors will be corrected before printing. Final book will be...
... We have shown that if we take any two forces that act at the same point, acting at an angle of u to each other, the forces may be composed to obtain the resultant of these two forces. Furthermore, the resultant of any two forces is unique because there is only one parallelogram that can be formed wi ...
... We have shown that if we take any two forces that act at the same point, acting at an angle of u to each other, the forces may be composed to obtain the resultant of these two forces. Furthermore, the resultant of any two forces is unique because there is only one parallelogram that can be formed wi ...