Module 2 Lesson 1 Angles
... Give the most specific angle pair for angles 1 and 2. 1. complementary 2. adjacent 3. linear pair or supplementary ...
... Give the most specific angle pair for angles 1 and 2. 1. complementary 2. adjacent 3. linear pair or supplementary ...
Midterm Review
... 24. When enclosing 4 sides of a rectangle with a given perimeter, the maximum area is obtained when all four sides are _____________________. 25. When enclosing 3 sides of a rectangle with a given perimeter, the maximum area is obtained when the sides have the following ratio: _____________________. ...
... 24. When enclosing 4 sides of a rectangle with a given perimeter, the maximum area is obtained when all four sides are _____________________. 25. When enclosing 3 sides of a rectangle with a given perimeter, the maximum area is obtained when the sides have the following ratio: _____________________. ...
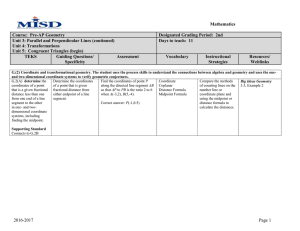
2nd Unit 3: Parallel and Perpendicular Lines
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
Basic Geometry
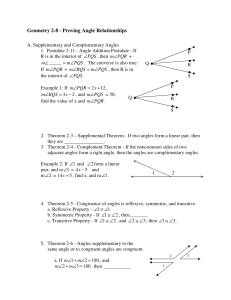
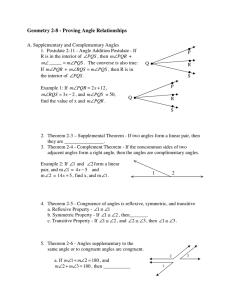
... 2. Two angles are _________________ if their measures have a sum of 90°. 3. When two rays intersect with a common endpoint a(n) _________________is formed. 4. The ________________ is the point located halfway between the endpoints of a segment. 5. _________________ are nonadjacent angles formed by t ...
... 2. Two angles are _________________ if their measures have a sum of 90°. 3. When two rays intersect with a common endpoint a(n) _________________is formed. 4. The ________________ is the point located halfway between the endpoints of a segment. 5. _________________ are nonadjacent angles formed by t ...