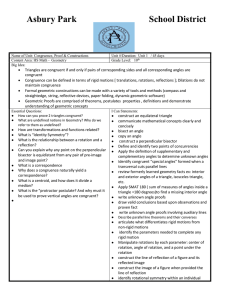
Aim #1 - Manhasset Schools
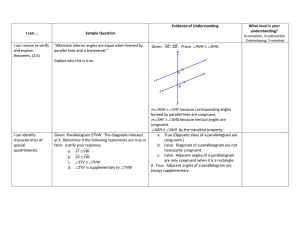
... The sum of angles on a straight line is 180° and two such ≮s are called a linear pair. A linear pair of ≮s are two adjacent ≮s whose non-common sides form a straight line. Two ≮s are called supplementary if the sum of their measures is __________; two ≮s are called complementary if the sum of their ...
... The sum of angles on a straight line is 180° and two such ≮s are called a linear pair. A linear pair of ≮s are two adjacent ≮s whose non-common sides form a straight line. Two ≮s are called supplementary if the sum of their measures is __________; two ≮s are called complementary if the sum of their ...
1.5 - Fairfield Public Schools
... Student Target: Students will be able to identify adjacent, vertical, complementary, supplementary angles, linear pairs, and angle bisectors and use their relationships to write equations to solve problems. Review: ...
... Student Target: Students will be able to identify adjacent, vertical, complementary, supplementary angles, linear pairs, and angle bisectors and use their relationships to write equations to solve problems. Review: ...