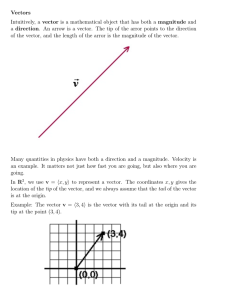
Angles
... An angle is the union of two rays that have a common endpoint. An angle can be named with the letter marking its vertex, B , and also with three letters: ABC- the first letter names a point on the side; the second names the vertex; the third names a point on the other side. A Vertex ...
... An angle is the union of two rays that have a common endpoint. An angle can be named with the letter marking its vertex, B , and also with three letters: ABC- the first letter names a point on the side; the second names the vertex; the third names a point on the other side. A Vertex ...
Basic Ideas of Geometry
... In our study, we will agree that a plane extends in all directions to infinity and is only one point thick A parallelogram is used to indicate a plane and shading helps to give the illusion that we are in 3 space ...
... In our study, we will agree that a plane extends in all directions to infinity and is only one point thick A parallelogram is used to indicate a plane and shading helps to give the illusion that we are in 3 space ...