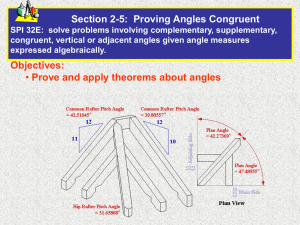
RCHS Rev. 06/2011 Geometry A Unit One Congruence Length of
... Power point presentations Sage and Scribe ...
... Power point presentations Sage and Scribe ...
Geometry Summer Institute 2014 Parallel Lines and Angles
... transversal l with respect to the lines L1 and L2, and we have to prove that L1 ∥ L2. As before, let O be the midpoint of the segment P1P2 and let R be the 180-degree rotation around O. If the rotated image of L2 is denoted by R(L2) and the rotated image of D1 is denoted by C′, then R(L2) passes thr ...
... transversal l with respect to the lines L1 and L2, and we have to prove that L1 ∥ L2. As before, let O be the midpoint of the segment P1P2 and let R be the 180-degree rotation around O. If the rotated image of L2 is denoted by R(L2) and the rotated image of D1 is denoted by C′, then R(L2) passes thr ...
Grade 6 Math Circles Angles Introduction Review: Types of Angles
... The easiest way to think of corresponding angles is the “F pattern.” If you draw the letter “F”, backwards or forwards, on the transversal, then the angles on top or below the horizontal lines will be congruent. Opposite angles are angles that are opposite each other when two lines cross. Opposite a ...
... The easiest way to think of corresponding angles is the “F pattern.” If you draw the letter “F”, backwards or forwards, on the transversal, then the angles on top or below the horizontal lines will be congruent. Opposite angles are angles that are opposite each other when two lines cross. Opposite a ...