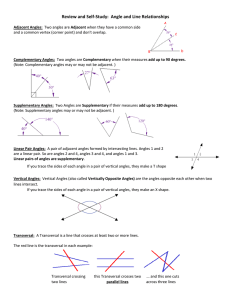
Alternate Interior Angles
... Corresponding Angles
Angles on the same side of the transversal and in the
same position on the parallel lines (either the angles are
both above or both below the parallel lines.)
Since the five types of angles describe angle relationships, we can
only classify PAIRS of angles as Alternate Interior ...
Rotation formalisms in three dimensions
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational (or angular) kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.According to Euler's rotation theorem the rotation of a rigid body (or three-dimensional coordinate system with the fixed origin) is described by a single rotation about some axis. Such a rotation may be uniquely described by a minimum of three real parameters. However, for various reasons, there are several ways to represent it. Many of these representations use more than the necessary minimum of three parameters, although each of them still has only three degrees of freedom.An example where rotation representation is used is in computer vision, where an automated observer needs to track a target. Let's consider a rigid body, with three orthogonal unit vectors fixed to its body (representing the three axes of the object's local coordinate system). The basic problem is to specify the orientation of these three unit vectors, and hence the rigid body, with respect to the observer's coordinate system, regarded as a reference placement in space.