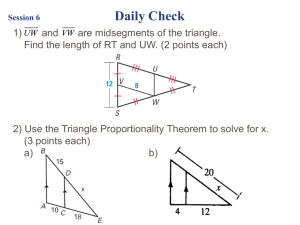
cpctc
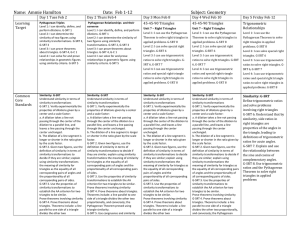
... Triangle Congruence: ASA, AAS, and Applying CPCTC Example 8: Writing a Proof Using CPCTC ...
... Triangle Congruence: ASA, AAS, and Applying CPCTC Example 8: Writing a Proof Using CPCTC ...
Chapter 4 Notes - Stevenson High School
... 1. Given the diagram below, list the congruent parts marked in the diagram. What additional information is needed to prove the two triangles congruent by AAS? ...
... 1. Given the diagram below, list the congruent parts marked in the diagram. What additional information is needed to prove the two triangles congruent by AAS? ...
File
... Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 5 ...
... Determine if whether each pair of triangles is congruent by SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 5 ...
Chapter-6 - ePathshala
... 6.6 TWO SPECIAL TRIANGLES : EQUILATERAL AND ISOSCELES A triangle in which all the three sides are of equal lengths is called an equilateral triangle. Take two copies of an equilateral triangle ABC (Fig 6.19). Keep one of them fixed. Place the second triangle on it. It fits exactly into the first. Tu ...
... 6.6 TWO SPECIAL TRIANGLES : EQUILATERAL AND ISOSCELES A triangle in which all the three sides are of equal lengths is called an equilateral triangle. Take two copies of an equilateral triangle ABC (Fig 6.19). Keep one of them fixed. Place the second triangle on it. It fits exactly into the first. Tu ...
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.