Geometry EOI Practice Trigonometric Ratios 1. If = 58° and m = 120
... NLM by the ASA theorem. Does Lisa's drawing prove ...
... NLM by the ASA theorem. Does Lisa's drawing prove ...
Origami building blocks: Generic and special four
... Equations 2(iii) and 3(iii) involve the two pairs of opposing plates, specifically addressing for which pair the sum of the sector angles is larger (and thus larger than π ). We call this pair the dominant pair, and we can use it to quickly identify the unique and binding plates of a generic vertex. ...
... Equations 2(iii) and 3(iii) involve the two pairs of opposing plates, specifically addressing for which pair the sum of the sector angles is larger (and thus larger than π ). We call this pair the dominant pair, and we can use it to quickly identify the unique and binding plates of a generic vertex. ...
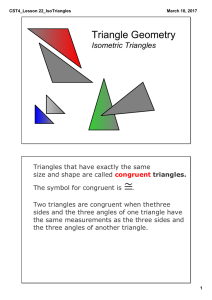
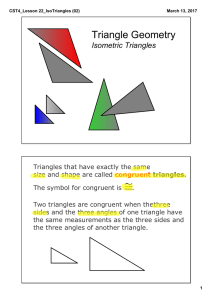
3 Congruent Triangles
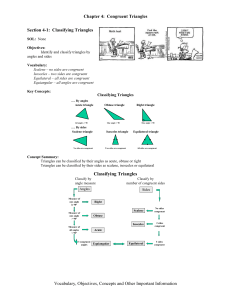
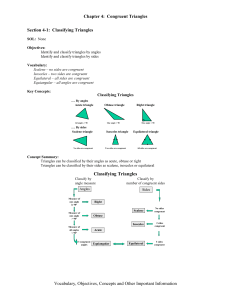
... • Two triangles are congruent if three sides of one triangle are equal to three sides of the other. (SSS) • Two triangles are congruent if two sides and the included angle of one triangle are equal to two sides and the included angle of the other. (SAS) • Two triangles are congruent if two angles an ...
... • Two triangles are congruent if three sides of one triangle are equal to three sides of the other. (SSS) • Two triangles are congruent if two sides and the included angle of one triangle are equal to two sides and the included angle of the other. (SAS) • Two triangles are congruent if two angles an ...
Origami building blocks: generic and special 4
... the folding motion and, in some cases, the number of folding branches. For example, the well-studied class of flat-foldable 4-vertices occurs when there is no dominant pair, i.e., when the sums of even and odd sector angles are equal. In that case, all folds close simultaneously. Clearly, qualitativ ...
... the folding motion and, in some cases, the number of folding branches. For example, the well-studied class of flat-foldable 4-vertices occurs when there is no dominant pair, i.e., when the sums of even and odd sector angles are equal. In that case, all folds close simultaneously. Clearly, qualitativ ...
Geometry Pre-AP – FBISD – 3rd 9 weeks 2013 – 2014 (Subject to
... patterns for special right triangles. Study guide – Case 1 & Case 2 (Begin Wednesday’s notes) ...
... patterns for special right triangles. Study guide – Case 1 & Case 2 (Begin Wednesday’s notes) ...
10 - Haiku Learning
... 18. A pair of obtuse angles can also be vertical angles. 19. A pair of straight angles can also be adjacent angles. ...
... 18. A pair of obtuse angles can also be vertical angles. 19. A pair of straight angles can also be adjacent angles. ...
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.