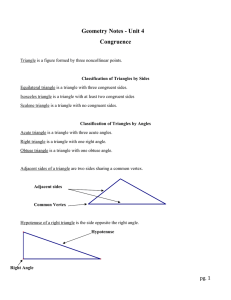
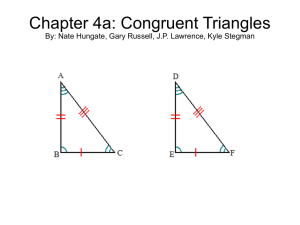
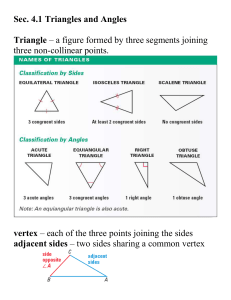
Unit 3.1 Congruent Triangles
... It would be difficult to establish that triangles were congruent if all six pairs of congruent parts had to first be verified. Fortunately, it is possible to prove triangles congruent by establishing fewer than six pairs of congruences. ...
... It would be difficult to establish that triangles were congruent if all six pairs of congruent parts had to first be verified. Fortunately, it is possible to prove triangles congruent by establishing fewer than six pairs of congruences. ...
Lesson #1 - Radical Tutor
... • SWBAT generate an infinite number of Pythagorean triples based on a given {a,b,c} triple • SWBAT generate an infinite number of Pythagorean triples using even numbers ...
... • SWBAT generate an infinite number of Pythagorean triples based on a given {a,b,c} triple • SWBAT generate an infinite number of Pythagorean triples using even numbers ...
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.