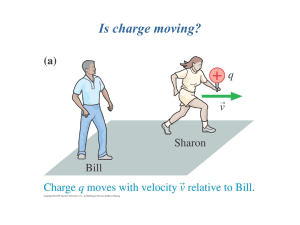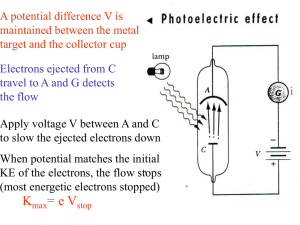
ppt - HEP Educational Outreach
... down to a single-photon (i.e. - there’s never more than a single photon in the apparatus at a time), what should we see? ...
... down to a single-photon (i.e. - there’s never more than a single photon in the apparatus at a time), what should we see? ...
No Slide Title
... emission spectrum that did not match known emission lines Mystery element was named Helium In 1895, William Ramsey discovered helium in a mineral of uranium (from alpha decay). ...
... emission spectrum that did not match known emission lines Mystery element was named Helium In 1895, William Ramsey discovered helium in a mineral of uranium (from alpha decay). ...
Materiality: Is It Real?
... which it is necessary to have practical explanations. Every physical substance has mass, or its essential existence . Its mass is what is pushed, pulled, spun, or just allowed to lie there, in terms of the practical aspects of our reality. It is an excellent “measurable” abstraction for use in the m ...
... which it is necessary to have practical explanations. Every physical substance has mass, or its essential existence . Its mass is what is pushed, pulled, spun, or just allowed to lie there, in terms of the practical aspects of our reality. It is an excellent “measurable” abstraction for use in the m ...
EE 5342 Lecture
... • E = hf, the quantum of energy for light. (PE effect & black body rad.) • f = c/l, c = 3E8m/sec, l = wavelength • From Poynting’s theorem (em waves), momentum density = energy density/c • Postulate a Photon “momentum” p = h/l = hk, h = h/2p wavenumber, k = 2p /l L1 January 20 ...
... • E = hf, the quantum of energy for light. (PE effect & black body rad.) • f = c/l, c = 3E8m/sec, l = wavelength • From Poynting’s theorem (em waves), momentum density = energy density/c • Postulate a Photon “momentum” p = h/l = hk, h = h/2p wavenumber, k = 2p /l L1 January 20 ...
Ch33 - Siena College
... Electromagnetic Waves Maxwell, using his equations of the electromagnetic field, was the first to understand that light is an oscillation of the electromagnetic field. Maxwell was able to predict that • Electromagnetic waves can exist at any frequency, not just at the frequencies of visible light. ...
... Electromagnetic Waves Maxwell, using his equations of the electromagnetic field, was the first to understand that light is an oscillation of the electromagnetic field. Maxwell was able to predict that • Electromagnetic waves can exist at any frequency, not just at the frequencies of visible light. ...
AP Physics HW Name: Photon Scattering and X
... The electron encounters a particle with the same mass and opposite charge (a positron) moving with the same speed in the opposite direction. The two particles undergo a head-on collision, which results in the disappearance of both particles and the production of two photons of the same energy. (c) D ...
... The electron encounters a particle with the same mass and opposite charge (a positron) moving with the same speed in the opposite direction. The two particles undergo a head-on collision, which results in the disappearance of both particles and the production of two photons of the same energy. (c) D ...
Atomic Spectra Bohr Model Notes
... Amplitude: height of the wave from the origin to the crest Wavelength ( ) : the distance between the crests (m, cm, nm) Frequency (v): number of waves to pass a given point per unit of time (waves/second = Hz) ...
... Amplitude: height of the wave from the origin to the crest Wavelength ( ) : the distance between the crests (m, cm, nm) Frequency (v): number of waves to pass a given point per unit of time (waves/second = Hz) ...
$doc.title
... Means that if we try to get fermions 1 and 2 into same state then ψ → 0 !!!! This is the Pauli Exclusion Principle: No two fermions (electrons) can have the same quantum state. ⇒ Can only have a spin up and a spin down electron in any atomic state N.B. in contrast, Bosons ‘like’ to be in same s ...
... Means that if we try to get fermions 1 and 2 into same state then ψ → 0 !!!! This is the Pauli Exclusion Principle: No two fermions (electrons) can have the same quantum state. ⇒ Can only have a spin up and a spin down electron in any atomic state N.B. in contrast, Bosons ‘like’ to be in same s ...
Light and the electron
... that electromagnetic radiation has both wavelike and particle-like natures. ► Extended upon Planck’s equation – photoelectric effect ► Pg. 124 practice problems 5,6 ...
... that electromagnetic radiation has both wavelike and particle-like natures. ► Extended upon Planck’s equation – photoelectric effect ► Pg. 124 practice problems 5,6 ...
3.5 Why does a quantum mechanic state change?
... The excited state may loose energy by the same processes as described above: • by electromagnetic radiation • the same particles, which moved into the solid, loose energy and momentum and will be detected in the scattered beam. • thermal processes (e.g. phonons) • at defects • on surfaces REMARK: Pr ...
... The excited state may loose energy by the same processes as described above: • by electromagnetic radiation • the same particles, which moved into the solid, loose energy and momentum and will be detected in the scattered beam. • thermal processes (e.g. phonons) • at defects • on surfaces REMARK: Pr ...
Chapter 27
... have the same speed because of the difference in their masses. For the same reason, remembering that KE = p2/2m, they cannot have the same kinetic energy. Because the kinetic energy is the only type of energy an isolated particle can have, and we have argued that the particles have different energie ...
... have the same speed because of the difference in their masses. For the same reason, remembering that KE = p2/2m, they cannot have the same kinetic energy. Because the kinetic energy is the only type of energy an isolated particle can have, and we have argued that the particles have different energie ...
Physics 5002 (Spring 2017) Discussion Problem (4/20) Consider
... The energy of the particle is E = h̄2 k 2 /(2m) > V0 . Take the incident wave to be exp(ikx) in the region of x < 0. 1. Derive the amplitude A of the reflected wave A exp(−ikx) in the region of x < 0. 2. Derive the amplitude D of the transmitted wave D exp[ik(x − L)] in the region of x > L. 3. Show ...
... The energy of the particle is E = h̄2 k 2 /(2m) > V0 . Take the incident wave to be exp(ikx) in the region of x < 0. 1. Derive the amplitude A of the reflected wave A exp(−ikx) in the region of x < 0. 2. Derive the amplitude D of the transmitted wave D exp[ik(x − L)] in the region of x > L. 3. Show ...
Quantum Theory 1 - Home Exercise 4
... (c) Show that for such a system, the energy eigenvalues must be integer multiples of 2π~/T . Hint : Assume the state ψ(x, t) has some defined energy E, then in article (c) show it must obey the condition given. 2. Consider a normalized wave function ψ(x). Assume that the system is in a state describ ...
... (c) Show that for such a system, the energy eigenvalues must be integer multiples of 2π~/T . Hint : Assume the state ψ(x, t) has some defined energy E, then in article (c) show it must obey the condition given. 2. Consider a normalized wave function ψ(x). Assume that the system is in a state describ ...
Homework set 1, due September 4, 11:40 am
... 5. (20 points) Consider a linearly polarized plane electromagnetic wave traveling in the +x-direction in free space having as its plane of vibration the xy plane. Given that its frequency is 10 MHz and its amplitude is E0= 0.08 V/m (a) Find the period and wavelength of the wave. (b) Write an express ...
... 5. (20 points) Consider a linearly polarized plane electromagnetic wave traveling in the +x-direction in free space having as its plane of vibration the xy plane. Given that its frequency is 10 MHz and its amplitude is E0= 0.08 V/m (a) Find the period and wavelength of the wave. (b) Write an express ...