Paper Folding And The Theorem of Pythagoras
... Can unfolding a paper boat reveal a proof of Pythagoras’ theorem? Does making a square within a square be anything more than an exercise in geometry at best? Art and math come together in delightful mathematical exercises described in this article. ...
... Can unfolding a paper boat reveal a proof of Pythagoras’ theorem? Does making a square within a square be anything more than an exercise in geometry at best? Art and math come together in delightful mathematical exercises described in this article. ...
Geometry and measures – Pick and mix revision cards
... circumference of a circle by the diameter? ...
... circumference of a circle by the diameter? ...
Introduction Right
... Complex numbers as points Now we have the machinery to look at complex number a different way. As we want to apply arithmetic to complex numbers, we should allow all things of the form a + bi, where a and b are real numbers. This looks like a point, with coordinates (a, b). In the rush to introduce ...
... Complex numbers as points Now we have the machinery to look at complex number a different way. As we want to apply arithmetic to complex numbers, we should allow all things of the form a + bi, where a and b are real numbers. This looks like a point, with coordinates (a, b). In the rush to introduce ...
UNIT 3 Pythagoras` Theorem Activities
... The following rule can be used to calculate the perpendicular height of an equilateral triangle: perpendicular height = k × side length where k is a fixed number. Find k, correct to 2 decimal places, using the examples from the table in question 1. ...
... The following rule can be used to calculate the perpendicular height of an equilateral triangle: perpendicular height = k × side length where k is a fixed number. Find k, correct to 2 decimal places, using the examples from the table in question 1. ...
A Guide to Advanced Euclidean Geometry
... Mindset suggests a number of ways to use the video lessons. These include: Watch or show a lesson as an introduction to a lesson Watch of show a lesson after a lesson, as a summary or as a way of adding in some interesting real-life applications or practical aspects Design a worksheet or set o ...
... Mindset suggests a number of ways to use the video lessons. These include: Watch or show a lesson as an introduction to a lesson Watch of show a lesson after a lesson, as a summary or as a way of adding in some interesting real-life applications or practical aspects Design a worksheet or set o ...
3/6 Quiz Review with reference sheet and answers File
... 9.1-9.3 Quiz Review Reference Materials 9.1 Similar Right Triangles ...
... 9.1-9.3 Quiz Review Reference Materials 9.1 Similar Right Triangles ...
A grade B student can …
... Use graphs to find the approximate solutions of quadratic equations Solve inequalities such as 3x < 9 and 12 ≤ 3n < 20 Solve linear inequalities such as 4x – 3 < 10 and 4x < 2x + 7 Represent sets of solutions on the number line Solve problems involving circles such as finding the perimeter of a semi ...
... Use graphs to find the approximate solutions of quadratic equations Solve inequalities such as 3x < 9 and 12 ≤ 3n < 20 Solve linear inequalities such as 4x – 3 < 10 and 4x < 2x + 7 Represent sets of solutions on the number line Solve problems involving circles such as finding the perimeter of a semi ...
Chapter 1. Classical Greek Mathematics
... and 17th centuries. It must be understood that many of the great discoveries in geometry were made about two and half thousand years ago. Given the difficulty of preserving fragile manuscripts, written on parchment or papyrus, over centuries when warfare could wipe out civilizations, it is not too s ...
... and 17th centuries. It must be understood that many of the great discoveries in geometry were made about two and half thousand years ago. Given the difficulty of preserving fragile manuscripts, written on parchment or papyrus, over centuries when warfare could wipe out civilizations, it is not too s ...
Puzzles and Pythagoras in the Classroom
... the integer symbols. In effect, all fractions were “unit fractions” or reciprocals. In our notation, all fractions were of the form ...
... the integer symbols. In effect, all fractions were “unit fractions” or reciprocals. In our notation, all fractions were of the form ...
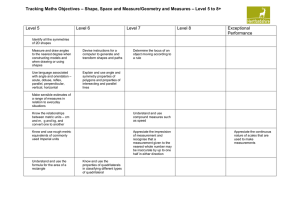
Tracking Shape, space and Measure/Geometry Learning Objectvies
... Appreciate the imprecision of measurement and recognise that a measurement given to the ...
... Appreciate the imprecision of measurement and recognise that a measurement given to the ...
GLOSSARY shape plane figure length width base vertical height
... Read pages 146, 147 and 150 to 155 (main features and properties of plane figures) Read pages 148 and 149 (Pythagoras’ Theorem) Read pages 156 and 158 (areas calculation) Read pages 170 to 179 (regular polyhedrons, cone, cylinder and sphere) Read page 184 (areas and volumes calculation) Read pages 1 ...
... Read pages 146, 147 and 150 to 155 (main features and properties of plane figures) Read pages 148 and 149 (Pythagoras’ Theorem) Read pages 156 and 158 (areas calculation) Read pages 170 to 179 (regular polyhedrons, cone, cylinder and sphere) Read page 184 (areas and volumes calculation) Read pages 1 ...
Saudi_Arabia_DAY_4PP - MSD-ORD
... (the "seeds" of the sequence) then assigning the rest by the rule that each number be the sum of the two preceding numbers. ...
... (the "seeds" of the sequence) then assigning the rest by the rule that each number be the sum of the two preceding numbers. ...
Notes on Greek Mathematics
... A Thales story [Heath p. 89]: He once fell into a well when stargazing, and was rescued by `a clever and pretty maidservant from Thrace’ (Plato) , who admonished him for being so eager to know what goes on in the heavens, he couldn’t see what was right in front of him. Pythagoras was born in Samos ( ...
... A Thales story [Heath p. 89]: He once fell into a well when stargazing, and was rescued by `a clever and pretty maidservant from Thrace’ (Plato) , who admonished him for being so eager to know what goes on in the heavens, he couldn’t see what was right in front of him. Pythagoras was born in Samos ( ...
MEI Structured Mathematics Practice Comprehension Question
... Pythagorean and other Triples Pythagoras was born on the Greek island of Samos in 572 BC and founded a school of philosophy, mathematics and natural science in the seaport of Crotona in Southern Italy. He is, of course, famous for the theorem that bears his name; that in a right-angled triangle the ...
... Pythagorean and other Triples Pythagoras was born on the Greek island of Samos in 572 BC and founded a school of philosophy, mathematics and natural science in the seaport of Crotona in Southern Italy. He is, of course, famous for the theorem that bears his name; that in a right-angled triangle the ...
Modern Geometries: Non-Euclidean, Projective, and Discrete
... http://cerezo.pntic.mec.es/mgarc144/marcohistoria/Modern%20Geometries.pdf ...
... http://cerezo.pntic.mec.es/mgarc144/marcohistoria/Modern%20Geometries.pdf ...
Nth Term - MathsBedwas
... so add algebra together and put equal to 360. • If perimeter, do the same but put = perimeter. • Solve by simplifying and ...
... so add algebra together and put equal to 360. • If perimeter, do the same but put = perimeter. • Solve by simplifying and ...
Proof Example: The Irrationality of √ 2 During the lecture a student
... conflict with him which finally escalated in sentencing him to death. (The school of Pythagoras had a strict code of conduct which included the penalty of death by drowning.) More details are at http://encyclopedia.thefreedictionary.com/Square+root+of+2. Remark 2. In order to keep the proof simple I ...
... conflict with him which finally escalated in sentencing him to death. (The school of Pythagoras had a strict code of conduct which included the penalty of death by drowning.) More details are at http://encyclopedia.thefreedictionary.com/Square+root+of+2. Remark 2. In order to keep the proof simple I ...
Lecture 4
... Octave in turn divided into ffth and fourth, with ratos 3:2 and 4:3 … up a ffth + up a fourth = up an octave. ffth … divided into three whole tones, each corresponding to the rato of 9:8 and a remainder with a rato of 256:243 fourth into two whole tones with same remainder. harmony… combinaton… of … ...
... Octave in turn divided into ffth and fourth, with ratos 3:2 and 4:3 … up a ffth + up a fourth = up an octave. ffth … divided into three whole tones, each corresponding to the rato of 9:8 and a remainder with a rato of 256:243 fourth into two whole tones with same remainder. harmony… combinaton… of … ...
Geometry Manual II TOC
... THE STUDY OF GEOMETRY: LEVEL II AN INTRODUCTION ........................................... 1 THE STUDY OF GEOMETRY: LEVEL II FLOW CHART ..................................................... 2 CHAPTER 1: CLASSIFIED NOMENCLATURE BASIC CONCEPTS - POINT, LINE, SURFACE, SOLID ........................... ...
... THE STUDY OF GEOMETRY: LEVEL II AN INTRODUCTION ........................................... 1 THE STUDY OF GEOMETRY: LEVEL II FLOW CHART ..................................................... 2 CHAPTER 1: CLASSIFIED NOMENCLATURE BASIC CONCEPTS - POINT, LINE, SURFACE, SOLID ........................... ...
Lecture4_FA16_greeks_solutions
... …it was better to learn none of the truth about mathematics, God, and the universe at all than to learn a little without learning all Pythagoreans … believed… when someone was "in doubt as to what he should say, he should always remain silent” Pythagoreans’ inner circle,“mathematikoi” ("mathematici ...
... …it was better to learn none of the truth about mathematics, God, and the universe at all than to learn a little without learning all Pythagoreans … believed… when someone was "in doubt as to what he should say, he should always remain silent” Pythagoreans’ inner circle,“mathematikoi” ("mathematici ...
music
... Mystic numbers • Pithagoras was a sort of ancient guru, who beguilled his followers with exotic doctrine of the trasmigration of the souls • The interest in number of the pitagoreans was more mystical than mathematics • The number was the key to the universe ...
... Mystic numbers • Pithagoras was a sort of ancient guru, who beguilled his followers with exotic doctrine of the trasmigration of the souls • The interest in number of the pitagoreans was more mystical than mathematics • The number was the key to the universe ...
music
... Mystic numbers • Pithagoras was a sort of ancient guru, who beguilled his followers with exotic doctrine of the trasmigration of the souls • The interest in number of the pitagoreans was more mystical than mathematics • The number was the key to the universe ...
... Mystic numbers • Pithagoras was a sort of ancient guru, who beguilled his followers with exotic doctrine of the trasmigration of the souls • The interest in number of the pitagoreans was more mystical than mathematics • The number was the key to the universe ...
Using Pythagoras to Calculate the Length of an Unknown Side
... squares. It is opposite the right angle so it is the Hypotenuse. The side with length 4 has 16 squares; it is sometimes called the Altitude. The side with length 3 can be called the Base and has 9 squares. Their squares (16 + 9) add up to 25 squares = the same as the number of squares off the hypote ...
... squares. It is opposite the right angle so it is the Hypotenuse. The side with length 4 has 16 squares; it is sometimes called the Altitude. The side with length 3 can be called the Base and has 9 squares. Their squares (16 + 9) add up to 25 squares = the same as the number of squares off the hypote ...
Pythagoras

Pythagoras of Samos (US /pɪˈθæɡərəs/; UK /paɪˈθæɡərəs/; Greek: Πυθαγόρας ὁ Σάμιος Pythagóras ho Sámios ""Pythagoras the Samian"", or simply Πυθαγόρας; Πυθαγόρης in Ionian Greek; c. 570 – c. 495 BC) was an Ionian Greek philosopher, mathematician, and has been credited as the founder of the movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him. He was born on the island of Samos, and traveled, visiting Egypt and Greece, and maybe India, and in 520 BC returned to Samos. Around 530 BC, he moved to Croton, in Magna Graecia, and there established some kind of school or guild.Pythagoras made influential contributions to philosophy and religion in the late 6th century BC. He is often revered as a great mathematician and scientist and is best known for the Pythagorean theorem which bears his name. However, because legend and obfuscation cloud his work even more than that of the other pre-Socratic philosophers, one can give only a tentative account of his teachings, and some have questioned whether he contributed much to mathematics or natural philosophy. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues and successors. Some accounts mention that the philosophy associated with Pythagoras was related to mathematics and that numbers were important. It was said that he was the first man to call himself a philosopher, or lover of wisdom, and Pythagorean ideas exercised a marked influence on Plato, and through him, all of Western philosophy.