D16/B330/3C11 Functional Programming Lecture 5
... But lists are special - they are RECURSIVE Data can be recursive, just like functions! ...
... But lists are special - they are RECURSIVE Data can be recursive, just like functions! ...
Example - bYTEBoss
... Developed at Utrecht University (Netherlands) Focuses on making learning Haskell easier Uses very clear and concise error messages. However, in order to make debugging easier, it has actually disabled many features of the language. ...
... Developed at Utrecht University (Netherlands) Focuses on making learning Haskell easier Uses very clear and concise error messages. However, in order to make debugging easier, it has actually disabled many features of the language. ...
Recursion
... Iterative control structures use a looping structure to repeat a set of statements. ...
... Iterative control structures use a looping structure to repeat a set of statements. ...
SECTION 10.3 LECTURE NOTES
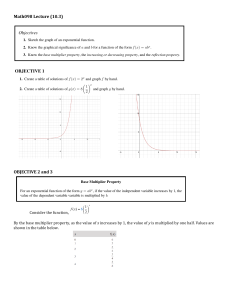
... 8 a and and g by hand. Use a graphing calculator to verify your graphs2in Problems 1 and 2. 3. Know the base multiplier property, the increasing or decreasing property, and the✓reflection property. ◆x Use a graphing calculator to verify your graphs in Problems 1 and 2. ...
... 8 a and and g by hand. Use a graphing calculator to verify your graphs2in Problems 1 and 2. 3. Know the base multiplier property, the increasing or decreasing property, and the✓reflection property. ◆x Use a graphing calculator to verify your graphs in Problems 1 and 2. ...
Chapter 1 - eLisa UGM
... • The basic process of computation is fundamentally different in a FPL than in an imperative language – In an imperative language, operations are done and the results are stored in variables for later use – Management of variables is a constant concern and source of complexity for imperative program ...
... • The basic process of computation is fundamentally different in a FPL than in an imperative language – In an imperative language, operations are done and the results are stored in variables for later use – Management of variables is a constant concern and source of complexity for imperative program ...
pl9ch15 - Systems and Computer Engineering
... • The basic process of computation is fundamentally different in a FPL than in an imperative language – In an imperative language, operations are done and the results are stored in variables for later use – Management of variables is a constant concern and source of complexity for imperative program ...
... • The basic process of computation is fundamentally different in a FPL than in an imperative language – In an imperative language, operations are done and the results are stored in variables for later use – Management of variables is a constant concern and source of complexity for imperative program ...
The current topic: Scheme Announcements Review: car, cdr, and
... • Some things evaluate to themselves. For these things, quoting has no effect (and is unnecessary). ...
... • Some things evaluate to themselves. For these things, quoting has no effect (and is unnecessary). ...
Variance and Standard Deviation - Penn Math
... Expected value for a binomial random variable For X a binomial random variable with parameters n and p ...
... Expected value for a binomial random variable For X a binomial random variable with parameters n and p ...
Lecture - 12: The RPAL Functional Language
... • Note the and keyword: not a boolean operator (for that we have &). ...
... • Note the and keyword: not a boolean operator (for that we have &). ...
lecture6-tau-private
... Note that we do not need to change our program anywhere else. מבוא מורחב ...
... Note that we do not need to change our program anywhere else. מבוא מורחב ...
- Starter tutorials
... • LISP functions specified using the above notation are called as S-expressions or symbolic expressions. • An S-expression can be either an atom or a list. • McCarthy developed a universal function capable of evaluating any other function. It was named EVAL. Vishnu Institute of technology – Website: ...
... • LISP functions specified using the above notation are called as S-expressions or symbolic expressions. • An S-expression can be either an atom or a list. • McCarthy developed a universal function capable of evaluating any other function. It was named EVAL. Vishnu Institute of technology – Website: ...
Lecture 07 - University of Florida
... • Note the and keyword: not a boolean operator (for that we have &). ...
... • Note the and keyword: not a boolean operator (for that we have &). ...
Ch. 15
... – Efficiency is the primary concern, rather than the suitability of the language for software development ...
... – Efficiency is the primary concern, rather than the suitability of the language for software development ...
x + 1 - Postech
... Variables are NOT variable. • The contents of a variable never change. • Surprise? – That’s because you are thinking about variables in imperative programming. variables in SML ...
... Variables are NOT variable. • The contents of a variable never change. • Surprise? – That’s because you are thinking about variables in imperative programming. variables in SML ...