Pauli Exclusion Principle Quiz
... Pauli Exclusion Principle Quiz 1. The location of any electron in an atom can be described by ____ unique quantum numbers. ...
... Pauli Exclusion Principle Quiz 1. The location of any electron in an atom can be described by ____ unique quantum numbers. ...
Jort Bergfeld : Completeness for a quantum hybrid logic.
... operator expressing non-orthogonality, @_i operators to express truth at a fixed state i and a "down arrow" to name the current state. QHL is an extension of the logic for quantum actions (LQA) introduced by Baltag and Smets and we will show all logical operators of LQA can be expressed in QHL. Quan ...
... operator expressing non-orthogonality, @_i operators to express truth at a fixed state i and a "down arrow" to name the current state. QHL is an extension of the logic for quantum actions (LQA) introduced by Baltag and Smets and we will show all logical operators of LQA can be expressed in QHL. Quan ...
Subject Group of Applied Physics
... Description and rationale: The aim of this course is to provide some fundamental knowledge and practical tools in quantum theory in order to explain various interesting phenomena reflecting the nature of the electron as a wave, or not as a particle. Only a few assumptions on each problem setup lead ...
... Description and rationale: The aim of this course is to provide some fundamental knowledge and practical tools in quantum theory in order to explain various interesting phenomena reflecting the nature of the electron as a wave, or not as a particle. Only a few assumptions on each problem setup lead ...
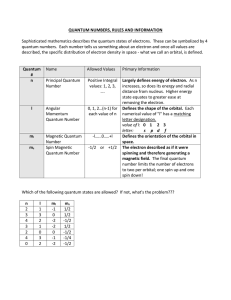
Quantum Number Table
... Sophisticated mathematics describes the quantum states of electrons. These can be symbolized by 4 quantum numbers. Each number tells us something about an electron and once all values are described, the specific distribution of electron density in space - what we call an orbital, is defined. ...
... Sophisticated mathematics describes the quantum states of electrons. These can be symbolized by 4 quantum numbers. Each number tells us something about an electron and once all values are described, the specific distribution of electron density in space - what we call an orbital, is defined. ...
Nondegenerate Pairings First let`s straighten out something that was
... Show that g is nondegenerate. Any algebra has a pairing of the above form; if the pairing is nondegenerate the algebra is semisimple. This is either a definition or a theorem depending on your taste: if we define a semisimple algebra to be a direct sum of algebras with no nontrivial two-sided ideals ...
... Show that g is nondegenerate. Any algebra has a pairing of the above form; if the pairing is nondegenerate the algebra is semisimple. This is either a definition or a theorem depending on your taste: if we define a semisimple algebra to be a direct sum of algebras with no nontrivial two-sided ideals ...
Department of Physics and Physical Oceanography Sigma Pi Sigma INDUCTION
... Department of Physics, Yeshiva University ...
... Department of Physics, Yeshiva University ...
Link between the hierarchy of fractional quantum Hall states and
... Link between the hierarchy of fractional quantum Hall states and Haldane’s conjecture for quantum spin chains Masaaki Nakamura Department of Physics, Tokyo Institute of Technology, Tokyo 152-8551, Japan ...
... Link between the hierarchy of fractional quantum Hall states and Haldane’s conjecture for quantum spin chains Masaaki Nakamura Department of Physics, Tokyo Institute of Technology, Tokyo 152-8551, Japan ...