CARLOS AUGUSTO DI PRISCO The notion of infinite appears in
... The construction of the model M [g] and the proof that it has the desired properties is quite elaborate. Certain elements of the model M are used as “names” for elements of M [g]. Which set is the object named by a name τ depends on the generic g, and given g, the model M [g] is the collection of se ...
... The construction of the model M [g] and the proof that it has the desired properties is quite elaborate. Certain elements of the model M are used as “names” for elements of M [g]. Which set is the object named by a name τ depends on the generic g, and given g, the model M [g] is the collection of se ...
3463: Mathematical Logic
... Because the encoding string y should end in a long string of 1s, there is at most one such factorisation possible. The Halting Problem is to decide whether a Turing machine halts on a given input. That is, HALTING = {yz : Ty exists and halts on input z}. Note that for any string x, there exists at m ...
... Because the encoding string y should end in a long string of 1s, there is at most one such factorisation possible. The Halting Problem is to decide whether a Turing machine halts on a given input. That is, HALTING = {yz : Ty exists and halts on input z}. Note that for any string x, there exists at m ...
Predicate logic
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
Predicate logic - Teaching-WIKI
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
Predicate logic
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
Lecture 3
... • Our scientific theories about the world can be expressed using mathematics and logic. The models of these theories often match the actual world is some way. But our scientific theories can be wrong. ...
... • Our scientific theories about the world can be expressed using mathematics and logic. The models of these theories often match the actual world is some way. But our scientific theories can be wrong. ...
Propositional Logic: Part I - Semantics
... “If pigs could fly then I’d enjoy brussel sprouts!” p : Pigs fly; b : Enjoy sprouts This (p |= b) is an invalid argument. Why use it? The real argument is: p, ¬p |= b which is a valid argument. Why is it valid? There is no counter example where p ∧ ¬p is true and b is false. Ex falso quod libet! i. ...
... “If pigs could fly then I’d enjoy brussel sprouts!” p : Pigs fly; b : Enjoy sprouts This (p |= b) is an invalid argument. Why use it? The real argument is: p, ¬p |= b which is a valid argument. Why is it valid? There is no counter example where p ∧ ¬p is true and b is false. Ex falso quod libet! i. ...
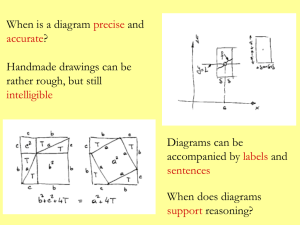
Diagrams in logic and mathematics - CFCUL
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
... “the laws of logic are not sculpted in stone, eternal and immutable. A realistic look at the development of mathematics shows that the reasons for a theorem are found only after digging deep and focusing upon the possibility of a theorem. The discovery of such hidden reasons is the work of the mathe ...
Predicate Logic
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables • First-order modal logic has extra modal operators with meanings which can be characterised informally as, for e ...
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables • First-order modal logic has extra modal operators with meanings which can be characterised informally as, for e ...
03_Artificial_Intelligence-PredicateLogic
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...
... • Infinitary logic allows infinitely long sentences; for example, one may allow a conjunction or disjunction of infinitely many formulas, or quantification over infinitely many variables ...