Problem set 7
... Problem set 7 Due by beginning of class on Monday Mar 5, 2012 BCH formula for x and p , SHO 1. Consider the function f (t) = etA Be−tA where A, B are a pair of operators (e.g. position and momentum or creation and annihilation operators etc.). t is a parameter which could be a time interval or a spa ...
... Problem set 7 Due by beginning of class on Monday Mar 5, 2012 BCH formula for x and p , SHO 1. Consider the function f (t) = etA Be−tA where A, B are a pair of operators (e.g. position and momentum or creation and annihilation operators etc.). t is a parameter which could be a time interval or a spa ...
A1982PH16500001
... Also, we tried to limit the material to the essential parts of a very difficult subject: many deep and wonderful technical results of the theory had to be omitted because they concerned ‘internal’ matters, and would not be appreciated by outsiders. This severe self-discipline made the book accessibl ...
... Also, we tried to limit the material to the essential parts of a very difficult subject: many deep and wonderful technical results of the theory had to be omitted because they concerned ‘internal’ matters, and would not be appreciated by outsiders. This severe self-discipline made the book accessibl ...
Concepts introduced by the theories of relativity include
... measurement of the other value. This theory became known as the uncertainty principle, which prompted Albert Einstein's famous comment, "God does not play dice." ...
... measurement of the other value. This theory became known as the uncertainty principle, which prompted Albert Einstein's famous comment, "God does not play dice." ...
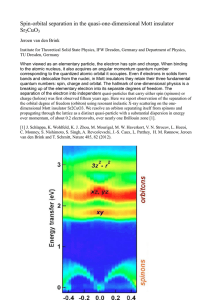
Spin-orbital separation in the quasi-one
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
Chapter 7 -- Radiative Corrections: some formal developments Chapter 7:
... everything in 1947 W.E. Lamb and R.C. Retherford decided to check results of Dirac. They used microwaves technique, available from the constructions of radar The Lamb's shift*, a minimal difference in lowest energetic level of the excited hydrogen atom can’t be explained in any way without introduct ...
... everything in 1947 W.E. Lamb and R.C. Retherford decided to check results of Dirac. They used microwaves technique, available from the constructions of radar The Lamb's shift*, a minimal difference in lowest energetic level of the excited hydrogen atom can’t be explained in any way without introduct ...
Desperately Seeking Superstrings
... day. A naive comparison of length scales suggests that to calculate the electron mass from superstrings would be a trillion times more difficult than to explain human behavior in terms of atomic physics. Superstring theory, unless it allows an approximation scheme for yielding useful and testable ph ...
... day. A naive comparison of length scales suggests that to calculate the electron mass from superstrings would be a trillion times more difficult than to explain human behavior in terms of atomic physics. Superstring theory, unless it allows an approximation scheme for yielding useful and testable ph ...
Some Families of Probability Distributions Within Quantum Theory
... “Some Families of Probability Distributions Within Quantum Theory” ...
... “Some Families of Probability Distributions Within Quantum Theory” ...
SCHRÖDINGER EQUATION FOR A PARTICLE ON A CURVED SPACE AND SUPERINTEGRABILITY
... momenta. Secondly, the Noether momenta do not Poisson commute classically, so the corresponding self-adjoint quantum operators do not commute. A planewave is more of a Euclidean concept, and its meaning needs to be clarified in a curved space. The approach taken here is mainly suited for discussing ...
... momenta. Secondly, the Noether momenta do not Poisson commute classically, so the corresponding self-adjoint quantum operators do not commute. A planewave is more of a Euclidean concept, and its meaning needs to be clarified in a curved space. The approach taken here is mainly suited for discussing ...
Course Title (1) Brief Course Description Modern Physics involves
... Modern Physics involves the extremes of very small distances and velocities close to the speed of light. These extremes demanded new theories in the early part of the 20th century and yielded the weird and wonderful results of Einstein’s relativity theory and Schrodinger’s equation in quantum mechan ...
... Modern Physics involves the extremes of very small distances and velocities close to the speed of light. These extremes demanded new theories in the early part of the 20th century and yielded the weird and wonderful results of Einstein’s relativity theory and Schrodinger’s equation in quantum mechan ...
... a. Find the partition function of an ideal gas of N diatomic molecules in which the two atoms don't interact with each other b. What is the energy of the gas? What is the heat capacity? c. How would the above change if the two atoms of each molecule interact with each other? Consider the interaction ...
CONJECTURING THE MATHEMATICAL AXIOM THAT
... Abstract. Combining the ideas of causality and the phenomenology of resonances and decaying states, we modify standard quantum theory by changing one of its axioms. The first step was taken decades ago when Dirac kets were given a mathematical meaning as functionals on a Schwartz space, which led to ...
... Abstract. Combining the ideas of causality and the phenomenology of resonances and decaying states, we modify standard quantum theory by changing one of its axioms. The first step was taken decades ago when Dirac kets were given a mathematical meaning as functionals on a Schwartz space, which led to ...
Transparancies for Revision Lecture - University of Manchester
... Sum of orbital and spin Anomalous Zeeman effect / Stern-Gerlach Expt ...
... Sum of orbital and spin Anomalous Zeeman effect / Stern-Gerlach Expt ...
Percolation: A Simple Example of Renormalization
... evaporation and condensation of fluids (phase transitions). See Wilson (1983). The renormalization group got its name from its early applications in QFT. There, it appeared to be a rather ad hoc method of subtracting away unwanted infinities. The further allegation was that the procedure is so horre ...
... evaporation and condensation of fluids (phase transitions). See Wilson (1983). The renormalization group got its name from its early applications in QFT. There, it appeared to be a rather ad hoc method of subtracting away unwanted infinities. The further allegation was that the procedure is so horre ...
Riemannian method in quantum field theory about curved space-time
... Starting from a given Lorentz metric g~k on a space-time manifold M and a tube T of world lines along which observers may move, we describe an algorithm to obtain the quantum theory of scalar particles of mass m. Let ei denote the 4-velocities of the world lines, and let V~, s real, be a family o f ...
... Starting from a given Lorentz metric g~k on a space-time manifold M and a tube T of world lines along which observers may move, we describe an algorithm to obtain the quantum theory of scalar particles of mass m. Let ei denote the 4-velocities of the world lines, and let V~, s real, be a family o f ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.