Noncommutative Quantum Mechanics
... Obtain a phase-space formulation of a noncommutative extension of QM in arbitrary number of dimensions; Show that physical previsions are independent of the chosen SW map. ...
... Obtain a phase-space formulation of a noncommutative extension of QM in arbitrary number of dimensions; Show that physical previsions are independent of the chosen SW map. ...
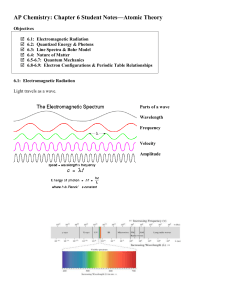
Chemistry 2000 Review: quantum mechanics of
... This equation was know to belong to a special class known as an eigenvector equation: an operator acts on a function (ψ) and generates a scalar times the same function Ψ is known as the wavefunction of the electron: there are an infinite number of such wavefunctions, each of which is characterized b ...
... This equation was know to belong to a special class known as an eigenvector equation: an operator acts on a function (ψ) and generates a scalar times the same function Ψ is known as the wavefunction of the electron: there are an infinite number of such wavefunctions, each of which is characterized b ...
Syllabus, Physics 315, Modern Physics, 3 credits Designation
... The concept of the wavefunction and its physical interpretation is introduced later in this chapter; there the Schrödinger equation appears, for a proper treatment of quantum dynamics. Some simple, one-dimensional cases are examined, with more complex examples following in Chapter 40, including the ...
... The concept of the wavefunction and its physical interpretation is introduced later in this chapter; there the Schrödinger equation appears, for a proper treatment of quantum dynamics. Some simple, one-dimensional cases are examined, with more complex examples following in Chapter 40, including the ...
Brooke R. Faulkner 1025 12
... Courses taken include: Quantum Mechanics I Mathematical Physics Solid State Physics ...
... Courses taken include: Quantum Mechanics I Mathematical Physics Solid State Physics ...
“SUPERPOSITION” “interference term”
... In simplest (“BCS”) theory, Cooper pairs, once formed, must automatically ...
... In simplest (“BCS”) theory, Cooper pairs, once formed, must automatically ...
Atomic, Molecular and Optical Physics
... four research labs and one theory group. Research infrastructure includes a number of titanium-sapphire, Nd:YAG, and precision diode laser systems, an ultracold quantum gases apparatus, and an ultrafast laser facility that supports joint AMO and condensed matter research. External collaborations inc ...
... four research labs and one theory group. Research infrastructure includes a number of titanium-sapphire, Nd:YAG, and precision diode laser systems, an ultracold quantum gases apparatus, and an ultrafast laser facility that supports joint AMO and condensed matter research. External collaborations inc ...
Module code SP-2301 Module Title Concepts in Modern Physics
... - Lorentz transformation equations to cover mechanics at all speeds, from which a basis for developing effects of relativity on other physical quantities like velocity, momentum, and energy will be established. - Development of the idea of rest energy and a new definition ...
... - Lorentz transformation equations to cover mechanics at all speeds, from which a basis for developing effects of relativity on other physical quantities like velocity, momentum, and energy will be established. - Development of the idea of rest energy and a new definition ...
Atlantis Studies in Mathematical Physics: Theory and Applications
... Topics include: Methods and applications of nonlinear differential and difference equations, classification and applications of integrable systems, integrability and geometry, dynamical systems, many-body problems, special functions of mathematical physics and q-analysis, symmetry analysis of differ ...
... Topics include: Methods and applications of nonlinear differential and difference equations, classification and applications of integrable systems, integrability and geometry, dynamical systems, many-body problems, special functions of mathematical physics and q-analysis, symmetry analysis of differ ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 2. Write down the Lorentz transformation equations between the proper velocities in two inertial frames for a boost along the common x-axis. 3. How does charge density transform under Lorentz transformation? 4. What is 4-potential in relativistic electromagnetism? 5. What is a Green’s function? 6. W ...
... 2. Write down the Lorentz transformation equations between the proper velocities in two inertial frames for a boost along the common x-axis. 3. How does charge density transform under Lorentz transformation? 4. What is 4-potential in relativistic electromagnetism? 5. What is a Green’s function? 6. W ...
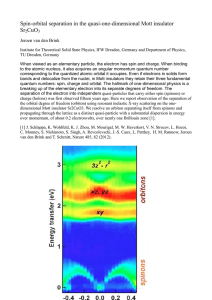
Spin-orbital separation in the quasi-one
... Sr2CuO3 Jeroen van den Brink Institute for Theoretical Solid State Physics, IFW Dresden, Germany and Department of Physics, TU Dresden, Germany When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum nu ...
... Sr2CuO3 Jeroen van den Brink Institute for Theoretical Solid State Physics, IFW Dresden, Germany and Department of Physics, TU Dresden, Germany When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum nu ...
Department of Physics PH101 Engineering Physics L-T-P-Cr: 3-1
... transformation, Length- contraction. Time Dilation, velocity addition, Mass change and Einstein’s mass – energy relation (A.B & 1.1,1.2,1.4 & 1.7-1.9 and appendix to chapter-1) Unit 6. Quantum Physics: Planck’s theory of black body radiation (.B & 2.3 & 9.5 &9.6) Compton effect (.B & 2.7) wave parti ...
... transformation, Length- contraction. Time Dilation, velocity addition, Mass change and Einstein’s mass – energy relation (A.B & 1.1,1.2,1.4 & 1.7-1.9 and appendix to chapter-1) Unit 6. Quantum Physics: Planck’s theory of black body radiation (.B & 2.3 & 9.5 &9.6) Compton effect (.B & 2.7) wave parti ...
of students from both classes could be
... an error was missed by Levi and by the editors and reviewers of the original paper. The observed change of 8.1 Sv is well within the uncertainty of the measurement. The correct conclusion from the data presented in Bryden’s paper should have been that no statistically significant change in Atlantic ...
... an error was missed by Levi and by the editors and reviewers of the original paper. The observed change of 8.1 Sv is well within the uncertainty of the measurement. The correct conclusion from the data presented in Bryden’s paper should have been that no statistically significant change in Atlantic ...
Max Born

Max Born (German: [bɔɐ̯n]; 11 December 1882 – 5 January 1970) was a German physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s. Born won the 1954 Nobel Prize in Physics for his ""fundamental research in Quantum Mechanics, especially in the statistical interpretation of the wave function"".Born was born in 1882 in Breslau, then in Germany, now in Poland and known as Wrocław. He entered the University of Göttingen in 1904, where he found the three renowned mathematicians, Felix Klein, David Hilbert and Hermann Minkowski. He wrote his Ph.D. thesis on the subject of ""Stability of Elastica in a Plane and Space"", winning the University's Philosophy Faculty Prize. In 1905, he began researching special relativity with Minkowski, and subsequently wrote his habilitation thesis on the Thomson model of the atom. A chance meeting with Fritz Haber in Berlin in 1918 led to discussion of the manner in which an ionic compound is formed when a metal reacts with a halogen, which is today known as the Born–Haber cycle.In the First World War after originally being placed as a radio operator, due to his specialist knowledge he was moved to research duties regarding sound ranging. In 1921, Born returned to Göttingen, arranging another chair for his long-time friend and colleague James Franck. Under Born, Göttingen became one of the world's foremost centres for physics. In 1925, Born and Werner Heisenberg formulated the matrix mechanics representation of quantum mechanics. The following year, he formulated the now-standard interpretation of the probability density function for ψ*ψ in the Schrödinger equation, for which he was awarded the Nobel Prize in 1954. His influence extended far beyond his own research. Max Delbrück, Siegfried Flügge, Friedrich Hund, Pascual Jordan, Maria Goeppert-Mayer, Lothar Wolfgang Nordheim, Robert Oppenheimer, and Victor Weisskopf all received their Ph.D. degrees under Born at Göttingen, and his assistants included Enrico Fermi, Werner Heisenberg, Gerhard Herzberg, Friedrich Hund, Pascual Jordan, Wolfgang Pauli, Léon Rosenfeld, Edward Teller, and Eugene Wigner.In January 1933, the Nazi Party came to power in Germany, and Born, who was Jewish, was suspended. He emigrated to Britain, where he took a job at St John's College, Cambridge, and wrote a popular science book, The Restless Universe, as well as Atomic Physics, which soon became a standard text book. In October 1936, he became the Tait Professor of Natural Philosophy at the University of Edinburgh, where, working with German-born assistants E. Walter Kellermann and Klaus Fuchs, he continued his research into physics. Max Born became a naturalised British subject on 31 August 1939, one day before World War II broke out in Europe. He remained at Edinburgh until 1952. He retired to Bad Pyrmont, in West Germany. He died in hospital in Göttingen on 5 January 1970.