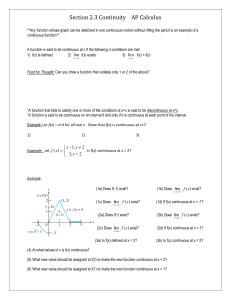
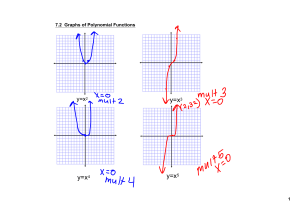
Section 2.3 Continuity AP Calculus - AP Calculus
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
First Order Predicate Logic
... • In addition to having terms, FOL has relational operators, which capture relationships between objects. • The language of FOL contains predicate symbols. • These symbols stand for relationships between objects. • Each predicate symbol has an associated arity (number of arguments). • Definition: Le ...
... • In addition to having terms, FOL has relational operators, which capture relationships between objects. • The language of FOL contains predicate symbols. • These symbols stand for relationships between objects. • Each predicate symbol has an associated arity (number of arguments). • Definition: Le ...
+ f
... CASE II f(x)> f(a) for some x in (a, b) [as in Figure l(b) or (c)] By the Extreme Value Theorem (which we can apply by hypothesis 1) f has a maximum value somewhere in [a, b]. Since f (a) = f (b), it must attain this maximum value at a number c in the open interval (a, b). Then f has a local maximum ...
... CASE II f(x)> f(a) for some x in (a, b) [as in Figure l(b) or (c)] By the Extreme Value Theorem (which we can apply by hypothesis 1) f has a maximum value somewhere in [a, b]. Since f (a) = f (b), it must attain this maximum value at a number c in the open interval (a, b). Then f has a local maximum ...
01. Simplest example phenomena
... and using unique factorization of positive integers into primes. This factorization produces an expression involving just primes equated to an expression not overtly involving primes. This hints at the relevance of the zeta function to prime numbers. The Euler product for ζ(s) is the entry to non-el ...
... and using unique factorization of positive integers into primes. This factorization produces an expression involving just primes equated to an expression not overtly involving primes. This hints at the relevance of the zeta function to prime numbers. The Euler product for ζ(s) is the entry to non-el ...
1 Distributions or generalized functions.
... We say that the sequence (ϕn ), ϕn ∈ D converges to zero if all this functions vanish outside a fixed interval I = [a, b], the same for all ϕn and converge to uniformly to zero together with their derivatives of any order. We say that a linear functional L ∈ D∗ is continuous if L(ϕn ) → 0 if ϕn conv ...
... We say that the sequence (ϕn ), ϕn ∈ D converges to zero if all this functions vanish outside a fixed interval I = [a, b], the same for all ϕn and converge to uniformly to zero together with their derivatives of any order. We say that a linear functional L ∈ D∗ is continuous if L(ϕn ) → 0 if ϕn conv ...
2.4 Continuity
... The kind of discontinuity illustrated in parts (a) and (c) is called removable because we could remove the discontinuity by redefining f at just the single number 2. [The function g(x) = x + 1 is continuous.] The discontinuity in part (b) is called an infinite discontinuity. The discontinuities in p ...
... The kind of discontinuity illustrated in parts (a) and (c) is called removable because we could remove the discontinuity by redefining f at just the single number 2. [The function g(x) = x + 1 is continuous.] The discontinuity in part (b) is called an infinite discontinuity. The discontinuities in p ...
Summer 2016 HW - APCalculus AB SummerReview_2016
... Solve by direct substitution whenever possible. If needed, rearrange the expression so that you can do direct substitution. ...
... Solve by direct substitution whenever possible. If needed, rearrange the expression so that you can do direct substitution. ...
Continuous functions( (الدوال المستمرة introduction The concept of
... The concept of continuous function is basic to much of mathematics .continuous functions on the real line appear in the first of any calculus book ,and continuous functions in the plane and in a space follow and far behind ,more general kinds of continuous functions arise as one goes further in math ...
... The concept of continuous function is basic to much of mathematics .continuous functions on the real line appear in the first of any calculus book ,and continuous functions in the plane and in a space follow and far behind ,more general kinds of continuous functions arise as one goes further in math ...