Download MAC 2233

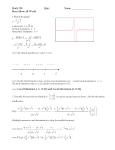
MAC 2233
Section 5.3
The Second Derivative and Analyzing Graphs
b.
c.
a.
d.
1. Order slopes of above lines, from the largest to the smallest in the sense that –7 is smaller
than –1.
______________
a.
b.
2. For the parabola in a above, is the slope of the
tangent increasing or decreasing?__________
So, is the second derivative (which is rate of
change of first derivative) positive or negative?
___________
3. For the parabola in b above, is the slope of the
tangent increasing or decreasing?__________
So, is the second derivative (which is rate of
change of first derivative) positive or negative?
_______________
DEFINITION OF CONCAVITY:
A curve is concave up on an open interval I if f ' , is increasing on I, and thus f  is positive on I.
A curve is concave down on an open interval I if f ' is decreasing on I, and thus f  is negative on I.
4 Are the parabolas above concave up or concave down? a.________________ b.________________
TEST FOR CONCAVITY:
If f ' ' is positive on an open interval I, then f is concave up because slope of tangent is increasing.
If f ' ' is negative on an open interval I, then f is concave down because slope of tangent is decreasing.
DEFINITION OF POINT OF INFLECTION:
A point of inflection is a point where the concavity of a curve changes—a point where f ' ' changes
“signs”—from positive to negative or negative to positive. A point of inflection occurs when f ' ' ( x) = 0.
FINDING POINTS OF INFLECTION:
Set the second derivative equal to 0 and solve for x. Substitute the x-value in the equation of the original
function to find the corresponding y-value. (A point of inflection may also occur at values of x for which
f ' ' is undefined, but we will not consider these cases.)
APPLICATIONS OF POINTS OF INFLECTION:
1. The minimum rate of change of a function (the point at which the function is decreasing most rapidly) occurs
at the “steepest” point of inflection for which the slope of the tangent is negative (thus function is decreasing.)
2. The maximum rate of change of a function (the point at which the function is increasing most rapidly) occurs
at the “steepest” point of inflection for which the slope of the tangent is positive (thus function is increasing.)
3. In economics, the point of inflection in (2) above, represents the point of diminishing returns for an inputoutput function with x being the input and y or f(x) being the output.
POINT OF DIMINISHING RETURNS:
The graph of the function below is to the right.
1
R=
(600 x 2  x 3 ) , 0  x  400
50,000
In the figure to the right, if x = c represents the point of inflection,
prior to x = c on the curve, each additional dollar of input returns
more than the previous input dollar. But when x is greater than c,
each additional dollar of input returns less than the previous input
dollar. An increased investment beyond this point is usually
considered a poor use of capital.
c
Homework: Page 324: odds 1 – 9, odds 17- 23, 35, 37, 39, 38, odds 61 – 67, two problems at the bottom of
this worksheet. On Problems: 35, 37, 38, 39, use your calculator to graph the function. Use first and second
derivatives to find relative and absolute extrema and points of inflection. Sketch graph on your paper labeling
these points.
For 2 and 3 below, identify the point of diminishing returns for the input-output function. For each function, R
is the revenue in thousands of dollars and x is the amount spent on advertising in thousands of dollars.
Remember: the point of diminishing returns is a point of inflection. Graph to verify your results. Sketch graph
& label point of diminishing returns.
4
1
1. R =
2. R = - (x3 – 9x2 – 27), 0  x  5
(600 x 2  x 3 ) , 0  x  400
9
50,000
(051)