Download Calc04_2_Briggs

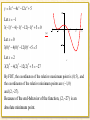
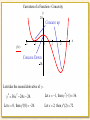
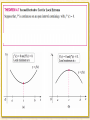
Blaise Pascal
1623 – 1662
Blaise Pascal was a very influential French mathematician and philosopher who
contributed to many areas of mathematics. He worked on conic sections and
projective geometry and in correspondence with Fermat he laid the foundations for
the theory of probability.
The First Derivative Test
Suppose that c is a critical number of a continuous
function f ( x).
a) If f ( x) changes from positive to negative at c, then
f ( x) has a local maximum at c.
b) If f ( x) changes from negative to positive at c, then
f ( x) has a local minimum at c.
c) If f ( x) does not change sign at c, then f ( x) has
no local maximum or minimum at c.
Example:
Consider y  3 x 4  4 x 3  12 x 2  5.
a) Find the critical values for y.
b) Find intervals of increasing and decreasing.
c) Identify the coordinates of all the extrema, determine if they
are local or absolute.

 0  0
y  12 x3  12 x 2  24 x
1
Let y  0
0  y
x
2
0
20
12 x 3  12 x 2  24 x  0
12 x( x 2  x  2)  0
12 x( x  2)( x  1)  0
f (x )
2
1
0
1
20
Critical numbers: x  0, x  2, x  1
x
2
3
Example:
Consider y  3 x 4  4 x 3  12 x 2  5.
a) Find the critical values for y.
b) Find intervals of increasing and decreasing.
c) Identify the coordinates of all the extrema, determine if they
are local or absolute.
 0  0
y  12 x3  12 x 2  24 x
Let y  0
12 x 3  12 x 2  24 x  0
12 x( x 2  x  2)  0
12 x( x  2)( x  1)  0
Critical numbers: x  0, x  2, x  1
1

0  y
x
0
2
By IDT,
Increasing: x   1, 0 
Decreasing:
 2,  
x   , 1  0, 2 
y  3x 4  4 x3  12 x 2  5
20
Let x  1
3(1)4  4(1)3  12(1) 2  5  0
f (x )
2
1
0
1
2
3
Let x  0
3(0)4  4(0)3  12(0)2  5  5
Let x  2
20
x
3(2)4  4(2)3  12(2)2  5  27
By FDT, the coordinates of the relative maximum point is (0,5), and
the coordinates of the relative minimum points are ( 1,0)
and (2, 27).
Because of the end-behavior of the function, (2,27) is an
absolute minimum point.
Example:
Curvature of a Function - Concavity
y
20
Concave up
f (x )
2
1
0
1
2
3
x
Concave Down
20
Lets take the second derivative of y.
y  36 x 2  24 x  24.
Let x  0, then y (0)  24.
x
Let x  1, then y ( 1)  36.
Let x  2, then y (2)  72.
Example: Analyze y and y for the function y  x3  3x 2  4.
y  3 x 2  6 x
Set
y  0
Possible extrema at x  0, 2.

0
3x  6 x  0
x  0, 2

0

y
x
2
3x  x  2   0
0
2
By IDT,
Increasing: x   , 0 
 2,  
Decreasing: x   0, 2 
By FDT, the coordinates of a relative maximum point are (0, 4)
and the coordinates of a relative minimum point are (2, 0).
Because of end-behavior there are no absolute extrema.
Now lets examine concavity, and look for inflection points by
setting the second derivative equal to zero.
y  6 x  6
Possible inflection point at x  1.

0  6x  6
By CT,

y 
x
6  6x
1 x
0
1
y  0  6  0  6  6
negative
y  2  6  2  6  6
positive
Concave Upward: x  1,  
Concave Downward: x   ,1
By DIP, there is an inflection point at (1, 2) since the second
derivative changes from negative to positive.
Given a real number c in the domain of a continuous function y = f (x),
First derivative:
y(c) is positive
Curve is increasing.
IDT
y(c) is negative
Curve is decreasing.
y(c) is zero or
Possible local maximum or
minimum points.
undefined
FDT
Second derivative:
y(c) is positive
Curve is concave up.
y(c) is negative
Curve is concave down.
y(c) is zero or
Possible inflection point
(where concavity changes).
undefined
CT
DIP
Example: Find the extreme points for y  x3  3x 2  4.
y  3 x 2  6 x
y  3x( x  2)
Possible extrema at x = 0, 2.
y(0)  0 and y(2)  0.
We can use the Second Derivative Test:
y  6 x  6
y  0  6  0  6  6
y  2  6  2  6  6
Because the second derivative at
x = 0 is negative, the graph is concave
down and therefore (0,4) is a local
maximum point.
Because the second derivative at
x = 2 is positive, the graph is concave up
and therefore (2,0) is a local minimum
point.
Examples
Examples