glossary_3
... The x-axis and y-axis placed at a right angle at their zero points, also called the Cartesian coordinate system. ...
... The x-axis and y-axis placed at a right angle at their zero points, also called the Cartesian coordinate system. ...
vector
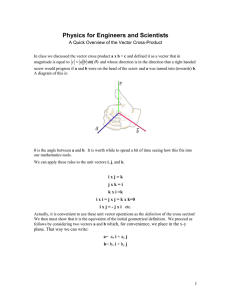
... standard unit vectors: the vectors i=<1, 0> and j=<0, 1> are unit vectors in the direction of the positive x-axis and y-axis respectively. linear combination: the expression v=ai+bj used to represent the vector
...
... standard unit vectors: the vectors i=<1, 0> and j=<0, 1> are unit vectors in the direction of the positive x-axis and y-axis respectively. linear combination: the expression v=ai+bj used to represent the vector
Grade 8 Geometry Review 1.(8G1a) Which sequence of
... Giselle will transform ∆XYZ shown below, using only rotations, reflections, and translations. ...
... Giselle will transform ∆XYZ shown below, using only rotations, reflections, and translations. ...
Geometry review, part I Geometry review I
... For computations, vectors can be described as pairs (2D), triples (3D), … of numbers. Coordinate system (2D) = point (origin) + 2 basis vectors. Orthogonal coordinate system: basis vectors perpendicular. Orthonormal coordinate system: basis vectors perpendicular and of unit length. Representation of ...
... For computations, vectors can be described as pairs (2D), triples (3D), … of numbers. Coordinate system (2D) = point (origin) + 2 basis vectors. Orthogonal coordinate system: basis vectors perpendicular. Orthonormal coordinate system: basis vectors perpendicular and of unit length. Representation of ...
Geometry and Constraints
... • At least one point must be specified • Direction may be specified with a second point or with an angle ...
... • At least one point must be specified • Direction may be specified with a second point or with an angle ...
The Coordinate Grid Lesson Plan
... A coordinate grid is a way to identify or describe any point on a flat surface, or plane, using a horizontal number line, the x-axes, with both positive and negative numbers, and a vertical number line, the y-axis. These axes form four quadrants, or sections; the number lines intersect at right angl ...
... A coordinate grid is a way to identify or describe any point on a flat surface, or plane, using a horizontal number line, the x-axes, with both positive and negative numbers, and a vertical number line, the y-axis. These axes form four quadrants, or sections; the number lines intersect at right angl ...
An angle inscribed in a semicircle is a right angle
... Proof. We shall view the points in the coordinate plane as vectors and relabel them as a, b, c, and x. Since x is the midpoint of a and b it follows that a − x = −(b − x). Let r = |a − x| = |b − x| = |c − x| . In vector language, the conclusion of the theorem is that a − c and b − c are perpendicula ...
... Proof. We shall view the points in the coordinate plane as vectors and relabel them as a, b, c, and x. Since x is the midpoint of a and b it follows that a − x = −(b − x). Let r = |a − x| = |b − x| = |c − x| . In vector language, the conclusion of the theorem is that a − c and b − c are perpendicula ...
Note Sheet 4-8
... Geometry 4-8 Triangles and Coordinate Proof A coordinate proof uses figures drawn in the coordinate plane and algebra to prove geometric concepts. There are four basic rules for placing your figures in the coordinate plane: Use the origin as a vertex or center of the triangle. Place at least one sid ...
... Geometry 4-8 Triangles and Coordinate Proof A coordinate proof uses figures drawn in the coordinate plane and algebra to prove geometric concepts. There are four basic rules for placing your figures in the coordinate plane: Use the origin as a vertex or center of the triangle. Place at least one sid ...
Exam 1 Material: Chapter 12
... Compute the cross product of two 3-D vectors Show that the resulting vector from the cross product is orthogonal to the original two vectors and determine which direction it points Determine the angle between two vectors using the cross product or express the magnitude of the cross product in ...
... Compute the cross product of two 3-D vectors Show that the resulting vector from the cross product is orthogonal to the original two vectors and determine which direction it points Determine the angle between two vectors using the cross product or express the magnitude of the cross product in ...
Sections 6.7-6.8 - Leon County Schools
... theorem (The midsegment of a trapezoid is parallel to the bases and its length is half the sum of the bases) ...
... theorem (The midsegment of a trapezoid is parallel to the bases and its length is half the sum of the bases) ...
Name Class Date Applying Coordinate Geometry Geometry
... Draw and label a square on a coordinate grid. In square ABCD, AB = BC = CD = DA. Draw in the diagonals, AC and BD . Prove that AC = BD. Use the Distance Formula. CA = (0 a)2 + (a 0)2 = a 2 + a 2 = 2a 2 BD = (a 0)2 + (a 0)2 = a 2 + a 2 = 2a 2 ...
... Draw and label a square on a coordinate grid. In square ABCD, AB = BC = CD = DA. Draw in the diagonals, AC and BD . Prove that AC = BD. Use the Distance Formula. CA = (0 a)2 + (a 0)2 = a 2 + a 2 = 2a 2 BD = (a 0)2 + (a 0)2 = a 2 + a 2 = 2a 2 ...
Rectangular Coordinate system Distance Between Two Points
... Find the coordinate of the point P , which is …ve-sixths of the distance from ( 7; 2) to ( 1; 4) : ...
... Find the coordinate of the point P , which is …ve-sixths of the distance from ( 7; 2) to ( 1; 4) : ...
Geometry Terms
... with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the first number indicates how far to travel from the origin in the direction of one axis, ...
... with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the first number indicates how far to travel from the origin in the direction of one axis, ...
Curvilinear coordinates
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible (a one-to-one map) at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.Well-known examples of curvilinear coordinate systems in three-dimensional Euclidean space (R3) are Cartesian, cylindrical and spherical polar coordinates. A Cartesian coordinate surface in this space is a plane; for example z = 0 defines the x-y plane. In the same space, the coordinate surface r = 1 in spherical polar coordinates is the surface of a unit sphere, which is curved. The formalism of curvilinear coordinates provides a unified and general description of the standard coordinate systems.Curvilinear coordinates are often used to define the location or distribution of physical quantities which may be, for example, scalars, vectors, or tensors. Mathematical expressions involving these quantities in vector calculus and tensor analysis (such as the gradient, divergence, curl, and Laplacian) can be transformed from one coordinate system to another, according to transformation rules for scalars, vectors, and tensors. Such expressions then become valid for any curvilinear coordinate system.Depending on the application, a curvilinear coordinate system may be simpler to use than the Cartesian coordinate system. For instance, a physical problem with spherical symmetry defined in R3 (for example, motion of particles under the influence of central forces) is usually easier to solve in spherical polar coordinates than in Cartesian coordinates. Equations with boundary conditions that follow coordinate surfaces for a particular curvilinear coordinate system may be easier to solve in that system. One would for instance describe the motion of a particle in a rectangular box in Cartesian coordinates, whereas one would prefer spherical coordinates for a particle in a sphere. Spherical coordinates are one of the most used curvilinear coordinate systems in such fields as Earth sciences, cartography, and physics (in particular quantum mechanics, relativity), and engineering.