QUESTIONS for latest set of presentations
... c. If a straight line falling on two straight lines makes the sum of the interior angles on the same side equal to two right angles then the two straight lines extend indefinitely and will never meet on either side. d. If two straight lines are cut by a transversal and the sum of the measure of the ...
... c. If a straight line falling on two straight lines makes the sum of the interior angles on the same side equal to two right angles then the two straight lines extend indefinitely and will never meet on either side. d. If two straight lines are cut by a transversal and the sum of the measure of the ...
Full text
... "instant millionaire" by winning a lottery. Recently, one of the authors was visiting relatives in Florida when a sequence of winning lottery numbers was announced. (In the Florida state lottery, one chooses six distinct integers from 1 to 49.) Someone suggested that a person might just as well choo ...
... "instant millionaire" by winning a lottery. Recently, one of the authors was visiting relatives in Florida when a sequence of winning lottery numbers was announced. (In the Florida state lottery, one chooses six distinct integers from 1 to 49.) Someone suggested that a person might just as well choo ...
Slide 1
... • We’ll be interested in the size of the column space now. • What do you think, is that space the whole four dimensional space? Just use your feeling, if we start with three vectors and take their combinations, can we get the whole four dimensional space? NO • So somehow we get a smaller space, but ...
... • We’ll be interested in the size of the column space now. • What do you think, is that space the whole four dimensional space? Just use your feeling, if we start with three vectors and take their combinations, can we get the whole four dimensional space? NO • So somehow we get a smaller space, but ...
Lecture 8 handout File
... framework for the problem (division into three cases) which is perhaps originally due to al-T . ūs.ī. We start by constructing a quadrilateral ABCD, (Fig. 2) with the angles at B and C both right angles, and the sides AB and CD equal. It’s then easy to show that the angles at A and D are equal. I ...
... framework for the problem (division into three cases) which is perhaps originally due to al-T . ūs.ī. We start by constructing a quadrilateral ABCD, (Fig. 2) with the angles at B and C both right angles, and the sides AB and CD equal. It’s then easy to show that the angles at A and D are equal. I ...
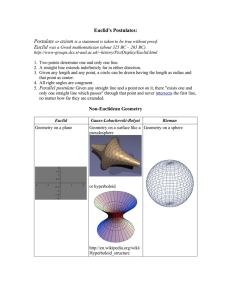
Euclid`s Postulates
... Euclid's Postulates: Postulate or axiom is a statement is taken to be true without proof. Euclid was a Greek mathematician (about 325 BC – 265 BC). http://www-groups.dcs.st-and.ac.uk/~history/PictDisplay/Euclid.html ...
... Euclid's Postulates: Postulate or axiom is a statement is taken to be true without proof. Euclid was a Greek mathematician (about 325 BC – 265 BC). http://www-groups.dcs.st-and.ac.uk/~history/PictDisplay/Euclid.html ...
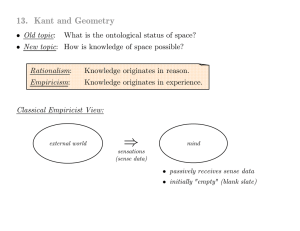
13.Kant and Geometry
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
Space Act - American Bar Association
... private actors to claim, any lifeforms discovered on other celestial bodies; additionally, by maintaining that the resources contemplated for use and extraction are “in situ” (rather than the asteroid itself), the Act may be countering fears that mining operations would be contrary to the prohibiti ...
... private actors to claim, any lifeforms discovered on other celestial bodies; additionally, by maintaining that the resources contemplated for use and extraction are “in situ” (rather than the asteroid itself), the Act may be countering fears that mining operations would be contrary to the prohibiti ...
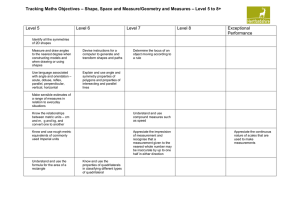
Tracking Shape, space and Measure/Geometry Learning Objectvies
... of measurement and recognise that a measurement given to the nearest whole number may be inaccurate by up to one half in either direction ...
... of measurement and recognise that a measurement given to the nearest whole number may be inaccurate by up to one half in either direction ...
The geometry of the universe - University of Maryland Astronomy
... that this triangle has three right angles, for a total of 270 degrees! How about a circle? Suppose we take the equator. Its circumference is 2πR, where R is the radius of the sphere. You might be tempted to say that its radius is R, but remember that we are confined to the surface, so the actual rad ...
... that this triangle has three right angles, for a total of 270 degrees! How about a circle? Suppose we take the equator. Its circumference is 2πR, where R is the radius of the sphere. You might be tempted to say that its radius is R, but remember that we are confined to the surface, so the actual rad ...
- Journal
... Iterative processes for the solutions of equations of various types are of common use in diversified fields. But the method gets little reflection when dealing with abstract spaces, e.g. supermetric space, metric space, Hilbert space etc. Approximate iterative solution of a class of functional equat ...
... Iterative processes for the solutions of equations of various types are of common use in diversified fields. But the method gets little reflection when dealing with abstract spaces, e.g. supermetric space, metric space, Hilbert space etc. Approximate iterative solution of a class of functional equat ...
Euclidean and Non-Euclidean Geometries: Development and History
... • “The effect of the discovery of hyperbolic geometry on our ideas of truth and reality have been so profound,” wrote the great Canadian geometer H.S.M. Coxeter, “that we can hardly imagine how shocking the possibility of a geometry different from Euclid’s must have seemed in 1820.” ...
... • “The effect of the discovery of hyperbolic geometry on our ideas of truth and reality have been so profound,” wrote the great Canadian geometer H.S.M. Coxeter, “that we can hardly imagine how shocking the possibility of a geometry different from Euclid’s must have seemed in 1820.” ...
Space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum known as spacetime. The concept of space is considered to be of fundamental importance to an understanding of the physical universe. However, disagreement continues between philosophers over whether it is itself an entity, a relationship between entities, or part of a conceptual framework.Debates concerning the nature, essence and the mode of existence of space date back to antiquity; namely, to treatises like the Timaeus of Plato, or Socrates in his reflections on what the Greeks called khôra (i.e. ""space""), or in the Physics of Aristotle (Book IV, Delta) in the definition of topos (i.e. place), or in the later ""geometrical conception of place"" as ""space qua extension"" in the Discourse on Place (Qawl fi al-Makan) of the 11th-century Arab polymath Alhazen. Many of these classical philosophical questions were discussed in the Renaissance and then reformulated in the 17th century, particularly during the early development of classical mechanics. In Isaac Newton's view, space was absolute—in the sense that it existed permanently and independently of whether there was any matter in the space. Other natural philosophers, notably Gottfried Leibniz, thought instead that space was in fact a collection of relations between objects, given by their distance and direction from one another. In the 18th century, the philosopher and theologian George Berkeley attempted to refute the ""visibility of spatial depth"" in his Essay Towards a New Theory of Vision. Later, the metaphysician Immanuel Kant said that neither space nor time can be empirically perceived—they are elements of a systematic framework that humans use to structure all experiences. Kant referred to ""space"" in his Critique of Pure Reason as being a subjective ""pure a priori form of intuition"", hence it is an unavoidable contribution of our human faculties.In the 19th and 20th centuries mathematicians began to examine geometries that are not Euclidean, in which space can be said to be curved, rather than flat. According to Albert Einstein's theory of general relativity, space around gravitational fields deviates from Euclidean space. Experimental tests of general relativity have confirmed that non-Euclidean geometries provide a better model for the shape of space.