Geometry - Hickman County Schools
... software such as Geometer’s Sketchpad and SPI 3108.2.2 Perform operations on vectors in ...
... software such as Geometer’s Sketchpad and SPI 3108.2.2 Perform operations on vectors in ...
Center for the Built Environment UC Berkeley
... Occupants’ satisfaction in office buildings is associated with indoor environmental quality (thermal, visual, acoustic environment and air quality) and workspace and building features including size, aesthetic appearance, furniture and cleanliness. The ten studies in Table 1 identified the parameter ...
... Occupants’ satisfaction in office buildings is associated with indoor environmental quality (thermal, visual, acoustic environment and air quality) and workspace and building features including size, aesthetic appearance, furniture and cleanliness. The ten studies in Table 1 identified the parameter ...
6.4 Notes
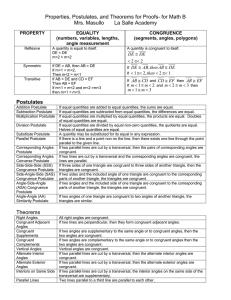
... If an angle of a quadrilateral is supplementary to both consecutive angles, then the quadrilateral is a parallelogram. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. If one pair of opposite sides of a quadrilateral are both congruent and paral ...
... If an angle of a quadrilateral is supplementary to both consecutive angles, then the quadrilateral is a parallelogram. If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. If one pair of opposite sides of a quadrilateral are both congruent and paral ...
Geo 4.3to4.5 DMW
... congruent by showing that all six pairs of corresponding parts were congruent. The property of triangle rigidity gives you a shortcut for proving two triangles congruent. It states that if the side lengths of a triangle are given, the triangle can have only one shape. ...
... congruent by showing that all six pairs of corresponding parts were congruent. The property of triangle rigidity gives you a shortcut for proving two triangles congruent. It states that if the side lengths of a triangle are given, the triangle can have only one shape. ...
congruent polygons
... Two polygons are congruent if and only if there is a correspondence between their sides and angles such that: 1. Each pair of corresponding angles is congruent. 2. Each pair of corresponding sides is congruent. homework Holt Geometry ...
... Two polygons are congruent if and only if there is a correspondence between their sides and angles such that: 1. Each pair of corresponding angles is congruent. 2. Each pair of corresponding sides is congruent. homework Holt Geometry ...
Word - The Open University
... (a) Through what angle do the students turn at A? (b) When they arrive at D, what is the total angle that they have turned through relative to their starting direction? (c) When they return to S, through what angle must they turn in order to face in the direction in which they started? (d) When ...
... (a) Through what angle do the students turn at A? (b) When they arrive at D, what is the total angle that they have turned through relative to their starting direction? (c) When they return to S, through what angle must they turn in order to face in the direction in which they started? (d) When ...
Constructive Geometry and the Parallel Postulate
... that, it is possible to connect it, just as in classical geometry, to the theory of Euclidean fields. A Euclidean field is an ordered field F in which non-negative elements have square roots. Classically, the models of elementary Euclidean geometry are planes F2 over a Euclidean field F. We show tha ...
... that, it is possible to connect it, just as in classical geometry, to the theory of Euclidean fields. A Euclidean field is an ordered field F in which non-negative elements have square roots. Classically, the models of elementary Euclidean geometry are planes F2 over a Euclidean field F. We show tha ...
Chapter 2 The Fifth Postulate
... We conclude that angle BST cannot be greater than angle CT S. In a similar way it can be shown that angle CT S cannot be greater than angle BST . The two angles must be equal and the first part of the proposition is proved. The remaining parts are then easily verified. There is evidence2 that the po ...
... We conclude that angle BST cannot be greater than angle CT S. In a similar way it can be shown that angle CT S cannot be greater than angle BST . The two angles must be equal and the first part of the proposition is proved. The remaining parts are then easily verified. There is evidence2 that the po ...
Symplectic structures -- a new approach to geometry.
... where the flux group Γω is a subgroup of H 1 (M, R). Example. In the case of the torus T 2 with a symplectic form dx ∧ dy of total area 1, the group Γω is H 1 (M, Z). The family of rotations Rt : (x, y) 7→ (x+t, y) of the torus T 2 consists of symplectomorphisms that are not Hamiltonian. Its image u ...
... where the flux group Γω is a subgroup of H 1 (M, R). Example. In the case of the torus T 2 with a symplectic form dx ∧ dy of total area 1, the group Γω is H 1 (M, Z). The family of rotations Rt : (x, y) 7→ (x+t, y) of the torus T 2 consists of symplectomorphisms that are not Hamiltonian. Its image u ...
Proving that a Quadrilateral is a Parallelogram Any of the methods
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...
... Name Honors Geometry Given: CirCle H and CirCle "Prove: HELO is a parallelogram ...
Geometry - Eleanor Roosevelt High School
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
... An indirect proof works because the negation of the statement to be proved is false, then we can conclude that the statement is true ...
Origami building blocks: Generic and special four
... is the simplest rigid-plated unit one can consider because it has just one continuous degree of freedom—vertices with fewer folds are fixed. Historically, the focus has been on flat-foldability, i.e., the situation where all folds can close simultaneously. In four-vertices, this is possible when the ...
... is the simplest rigid-plated unit one can consider because it has just one continuous degree of freedom—vertices with fewer folds are fixed. Historically, the focus has been on flat-foldability, i.e., the situation where all folds can close simultaneously. In four-vertices, this is possible when the ...
Space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum known as spacetime. The concept of space is considered to be of fundamental importance to an understanding of the physical universe. However, disagreement continues between philosophers over whether it is itself an entity, a relationship between entities, or part of a conceptual framework.Debates concerning the nature, essence and the mode of existence of space date back to antiquity; namely, to treatises like the Timaeus of Plato, or Socrates in his reflections on what the Greeks called khôra (i.e. ""space""), or in the Physics of Aristotle (Book IV, Delta) in the definition of topos (i.e. place), or in the later ""geometrical conception of place"" as ""space qua extension"" in the Discourse on Place (Qawl fi al-Makan) of the 11th-century Arab polymath Alhazen. Many of these classical philosophical questions were discussed in the Renaissance and then reformulated in the 17th century, particularly during the early development of classical mechanics. In Isaac Newton's view, space was absolute—in the sense that it existed permanently and independently of whether there was any matter in the space. Other natural philosophers, notably Gottfried Leibniz, thought instead that space was in fact a collection of relations between objects, given by their distance and direction from one another. In the 18th century, the philosopher and theologian George Berkeley attempted to refute the ""visibility of spatial depth"" in his Essay Towards a New Theory of Vision. Later, the metaphysician Immanuel Kant said that neither space nor time can be empirically perceived—they are elements of a systematic framework that humans use to structure all experiences. Kant referred to ""space"" in his Critique of Pure Reason as being a subjective ""pure a priori form of intuition"", hence it is an unavoidable contribution of our human faculties.In the 19th and 20th centuries mathematicians began to examine geometries that are not Euclidean, in which space can be said to be curved, rather than flat. According to Albert Einstein's theory of general relativity, space around gravitational fields deviates from Euclidean space. Experimental tests of general relativity have confirmed that non-Euclidean geometries provide a better model for the shape of space.