SYMMETRIES OF MONOCORONAL TILINGS 1. Introduction The
... Remark 2.3. It turns out that the 1-periodic tilings in Theorem 2.2 consist of 1-periodic layers that are stacked according to a non-periodic one-dimensional sequence (see for instance Figure 9, page 11). Such a sequence may look simply like . . . 1, 1, 1, 0, 1, 1, 1, . . . (all 1s, one 0) or, more ...
... Remark 2.3. It turns out that the 1-periodic tilings in Theorem 2.2 consist of 1-periodic layers that are stacked according to a non-periodic one-dimensional sequence (see for instance Figure 9, page 11). Such a sequence may look simply like . . . 1, 1, 1, 0, 1, 1, 1, . . . (all 1s, one 0) or, more ...
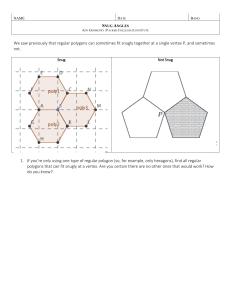
Angle and Regular Polygon Review
... onto the other colored half. Assume the original interior was white in color. The red half folds onto the orange half so that both halves match. This makes m a line of symmetry. What kind of line symmetry is this? l ...
... onto the other colored half. Assume the original interior was white in color. The red half folds onto the orange half so that both halves match. This makes m a line of symmetry. What kind of line symmetry is this? l ...
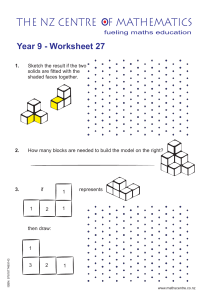
Word Problems
... ship her jewelry. She wants to shape the box like a regular polygon. In order for the boxes to pack tightly, she decides to use a regular polygon that has the property that the measure of its interior angles is half the measure of its exterior angles. What regular polygon should she use? ...
... ship her jewelry. She wants to shape the box like a regular polygon. In order for the boxes to pack tightly, she decides to use a regular polygon that has the property that the measure of its interior angles is half the measure of its exterior angles. What regular polygon should she use? ...
Answers for the lesson “Relate Transformations and Congruence”
... that share an edge can be rotated either 728 around the vertex of the smaller angle or 1088 around the vertex of the larger angle. Red tiles that share an edge can be rotated 368 around the vertex of the smaller angle or 1448 around the vertex of the larger angle. ...
... that share an edge can be rotated either 728 around the vertex of the smaller angle or 1088 around the vertex of the larger angle. Red tiles that share an edge can be rotated 368 around the vertex of the smaller angle or 1448 around the vertex of the larger angle. ...
Study Guide – Geometry
... - Measure angles up to 180 degrees - Classify these angles (acute, right, obtuse, straight). - Construct shapes (any polygon) given a set of instructions (angle measure, side length, type of polygon). Don’t forget to name each vertex! - Identifying line symmetry (how many lines of symmetry and where ...
... - Measure angles up to 180 degrees - Classify these angles (acute, right, obtuse, straight). - Construct shapes (any polygon) given a set of instructions (angle measure, side length, type of polygon). Don’t forget to name each vertex! - Identifying line symmetry (how many lines of symmetry and where ...
Math Quiz Alert Unit 3
... Draw a given shape. (Example: Draw an isosceles triangle that is not equilateral. Compare similar and different properties of triangles (Examples: Explain at least one way that scalene and equilateral triangles are different. Explain at least one way that isosceles and scalene triangles are the same ...
... Draw a given shape. (Example: Draw an isosceles triangle that is not equilateral. Compare similar and different properties of triangles (Examples: Explain at least one way that scalene and equilateral triangles are different. Explain at least one way that isosceles and scalene triangles are the same ...
Letters A-Z in math
... • A triangle with two sides that are the same length. Formally, an isosceles triangle is a triangle with at least two congruent sides. ...
... • A triangle with two sides that are the same length. Formally, an isosceles triangle is a triangle with at least two congruent sides. ...
Tessellation

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semi-regular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called ""non-periodic"". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern. In the geometry of higher dimensions, a space-filling or honeycomb is also called a tessellation of space.A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such tilings may be decorative patterns, or may have functions such as providing durable and water-resistant pavement, floor or wall coverings. Historically, tessellations were used in Ancient Rome and in Islamic art such as in the decorative tiling of the Alhambra palace. In the twentieth century, the work of M. C. Escher often made use of tessellations, both in ordinary Euclidean geometry and in hyperbolic geometry, for artistic effect. Tessellations are sometimes employed for decorative effect in quilting. Tessellations form a class of patterns in nature, for example in the arrays of hexagonal cells found in honeycombs.