Geometry Standards
... 1. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. 2. Derive the equation of a parabola given a focus and directrix. 3. (+) Derive the equations of ellipses and hyperbolas gi ...
... 1. Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. 2. Derive the equation of a parabola given a focus and directrix. 3. (+) Derive the equations of ellipses and hyperbolas gi ...
Document
... Another words, in the class of Hausdorff spaces, compactness is an absolute closeness. Ex 3. X is infinite set with finite complement topology. X is compact, since for any open cover, we fix one element of it, the complement is finite, so can be covered by finite many elements. And any subspace of X ...
... Another words, in the class of Hausdorff spaces, compactness is an absolute closeness. Ex 3. X is infinite set with finite complement topology. X is compact, since for any open cover, we fix one element of it, the complement is finite, so can be covered by finite many elements. And any subspace of X ...
GEOMETRIC SEARCHING PART 1: POINT LOCATION
... Left vertical side is defined by the segment end-point p=leftp(D) (a) common left point p itself (b) by the lower vert. extension of left point p ending at bottom() (c) by the upper vert. extension of left point p ending at top() (d) by both vert. extensions of the right point p (e) the left edge of ...
... Left vertical side is defined by the segment end-point p=leftp(D) (a) common left point p itself (b) by the lower vert. extension of left point p ending at bottom() (c) by the upper vert. extension of left point p ending at top() (d) by both vert. extensions of the right point p (e) the left edge of ...
2.1 inductive reasoning and conjecture ink.notebook
... make the first square? How many tiles do you have to add to the first square to get the second square? How many tiles do you have to add to the second square to get the third square? b) Make a conjecture about the list of numbers you started writing in your answer to Ex ...
... make the first square? How many tiles do you have to add to the first square to get the second square? How many tiles do you have to add to the second square to get the third square? b) Make a conjecture about the list of numbers you started writing in your answer to Ex ...
Geometry - Lakeview Public Schools
... analytic and spatial reasoning. They apply what they know about two-dimensional figures to three-dimensional figures in real-world contexts, building spatial visualization skills and deepening their understanding of shape and shape relationships. Geometry includes a study of right triangle trigonome ...
... analytic and spatial reasoning. They apply what they know about two-dimensional figures to three-dimensional figures in real-world contexts, building spatial visualization skills and deepening their understanding of shape and shape relationships. Geometry includes a study of right triangle trigonome ...
Chapter 1 Notes 2013
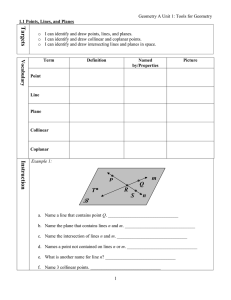
... Geometry Period _________ Directed Line Segment: Tells the direction in which from which point to start and end. In this case, from Point A to Point B What does that tell you about the distance AP and PB in relation to AB? ...
... Geometry Period _________ Directed Line Segment: Tells the direction in which from which point to start and end. In this case, from Point A to Point B What does that tell you about the distance AP and PB in relation to AB? ...
SCDE Standards suggested for inclusion CCSSM Geometry SC
... are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. G.C.4 (+) Construct a tangent line from a ...
... are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle. G.C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. G.C.4 (+) Construct a tangent line from a ...