H-CLOSED SPACES AND THE ASSOCIATED 9
... A convergence space is said to be compact if every maximal filterbase converges. Lemma. ...
... A convergence space is said to be compact if every maximal filterbase converges. Lemma. ...
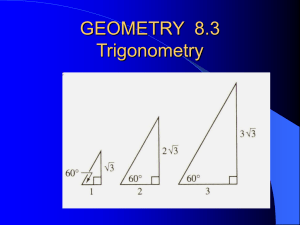
GEOMETRY 8.3 Trigonometry
... • Press ENTER to get degrees of the Angle. Use your Calculator to determine Angle A: If Side a = 5, and Hypotenuse c = 8 If Side a = 10, and Hypotenuse c = 40 If Side a = 15, and Hypotenuse c = 18 ...
... • Press ENTER to get degrees of the Angle. Use your Calculator to determine Angle A: If Side a = 5, and Hypotenuse c = 8 If Side a = 10, and Hypotenuse c = 40 If Side a = 15, and Hypotenuse c = 18 ...
Remarks on the Cartan Formula and Its Applications
... End(T ⊕ T ∗ ), which satisfies both symplectic and complex conditions, i.e. J ∗ = −J (equivalently, orthogonal with respect to the canonical inner product (4.1)) and J 2 = −1. We can show that the obstruction to the existence of a generalized almost complex structure is the same as that for an almos ...
... End(T ⊕ T ∗ ), which satisfies both symplectic and complex conditions, i.e. J ∗ = −J (equivalently, orthogonal with respect to the canonical inner product (4.1)) and J 2 = −1. We can show that the obstruction to the existence of a generalized almost complex structure is the same as that for an almos ...
11/10 Notes - Converse Theorems
... A second style of proof is a flowchart proof, which uses boxes and arrows to show the structure of the proof. The justification for each step is written below the box. ...
... A second style of proof is a flowchart proof, which uses boxes and arrows to show the structure of the proof. The justification for each step is written below the box. ...
C:\Documents and Settings\User\My Documents\Classes\362
... equal to the sum of the measures of each its remote interiors, its measure is the sum of their measures. We all know that the angle sum of a triangle in Euclidean geometry is not just less than or equal to 180, but in fact equal to 180. ...
... equal to the sum of the measures of each its remote interiors, its measure is the sum of their measures. We all know that the angle sum of a triangle in Euclidean geometry is not just less than or equal to 180, but in fact equal to 180. ...
A FIXED POINT THEOREM FOR BOUNDED
... We will prove the theorem for maps, and derive the theorem for flows as a consequence. In fact, many of the definitions and proofs follow analogously for both cases. When that is the case, we will just refer to the “dynamical system,” with the recognition that the statement applies to both flows and ...
... We will prove the theorem for maps, and derive the theorem for flows as a consequence. In fact, many of the definitions and proofs follow analogously for both cases. When that is the case, we will just refer to the “dynamical system,” with the recognition that the statement applies to both flows and ...
Matt Wolf - CB East Wolf
... Concerning the Inhabitants of Flatland THE GREATEST length or breadth of a full grown inhabitant of Flatland may be estimated at about eleven of your inches. Twelve inches may be regarded as a maximum. Our Women are Straight Lines. Our Soldiers and Lowest Class of Workmen are Triangles with two equa ...
... Concerning the Inhabitants of Flatland THE GREATEST length or breadth of a full grown inhabitant of Flatland may be estimated at about eleven of your inches. Twelve inches may be regarded as a maximum. Our Women are Straight Lines. Our Soldiers and Lowest Class of Workmen are Triangles with two equa ...
Unit 1
... See how many words your child can think of that have Greek/Latin prefixes such as tri-, quad-, penta-, hexa-, octa-, and so on. Help your child think of different ways to draw or make figures without the use of a compass, protractor, or straightedge. For example, you can trace the bottom of a ca ...
... See how many words your child can think of that have Greek/Latin prefixes such as tri-, quad-, penta-, hexa-, octa-, and so on. Help your child think of different ways to draw or make figures without the use of a compass, protractor, or straightedge. For example, you can trace the bottom of a ca ...
Concepts in Algebra and Geometry
... Much of the Algebra sequence that follows is already an informal part of Geometry B. But the formal and specific emphasis on these topics means that we will be unable to cover some of the current Geometry sequence. We believe that the Glencoe text mitigates this sacrifice by ensuring adequate covera ...
... Much of the Algebra sequence that follows is already an informal part of Geometry B. But the formal and specific emphasis on these topics means that we will be unable to cover some of the current Geometry sequence. We believe that the Glencoe text mitigates this sacrifice by ensuring adequate covera ...
Products, Quotients and Manifolds
... Exercise 6.12. Let π1 : R×R → R be projection onto the first coordinate: (x, y) 7→ x. Let A = {(x, y) ∈ R2 | x ≥ 0 or y = 0}. Let f = π1 |A : A → R. a) Show: f is quotient map. (Suggestion: use the previous exercise.) b) Show: f is neither open nor closed. Exercise 6.13. Let q : X → Y be a quotient m ...
... Exercise 6.12. Let π1 : R×R → R be projection onto the first coordinate: (x, y) 7→ x. Let A = {(x, y) ∈ R2 | x ≥ 0 or y = 0}. Let f = π1 |A : A → R. a) Show: f is quotient map. (Suggestion: use the previous exercise.) b) Show: f is neither open nor closed. Exercise 6.13. Let q : X → Y be a quotient m ...
Solutions to Midterm 2 Problem 1. Let X be Hausdorff and A ⊂ X
... Since X is Hausdorff, all Kα are closed and {X rKα } is an open covering of X rU . Take a finite subcovering; the corresponding Kα ’s are what we need. Solution: ...
... Since X is Hausdorff, all Kα are closed and {X rKα } is an open covering of X rU . Take a finite subcovering; the corresponding Kα ’s are what we need. Solution: ...
Explore Ratios, Proportions, and Equalities within a Triangle
... Explore Ratios, Proportions, and Equalities within a Triangle Directions: 1. Determine which statements are true. 2. Provide a counterexample for the statements that are false. 3. Conjecture and explore on your own to find additional true statements, or modify a statement to make it true. 4. Prove t ...
... Explore Ratios, Proportions, and Equalities within a Triangle Directions: 1. Determine which statements are true. 2. Provide a counterexample for the statements that are false. 3. Conjecture and explore on your own to find additional true statements, or modify a statement to make it true. 4. Prove t ...