Geometry 1 - spartansmath
... 38. Find the area of the rectangle with length of 8 and width 3.2. 39. If the vertex angle of an isosceles triangle measures 44°, what is the measure of each base angle? 40. If all four sides of a quadrilateral are congruent, the quadrilateral is a _______. 41. If all four angles of a quadrilateral ...
... 38. Find the area of the rectangle with length of 8 and width 3.2. 39. If the vertex angle of an isosceles triangle measures 44°, what is the measure of each base angle? 40. If all four sides of a quadrilateral are congruent, the quadrilateral is a _______. 41. If all four angles of a quadrilateral ...
SSS, SAS, AAS, ASA
... Determine the reason that ! NKL ≅! NJL . Then, find m∠J if m∠KLN = 20" . Because the two right triangles share a common side (a leg), segment NL, and we know that the hypotenuses are congruent, the two triangles are congruent by HL. Remember that means that all corresponding sides and angles are con ...
... Determine the reason that ! NKL ≅! NJL . Then, find m∠J if m∠KLN = 20" . Because the two right triangles share a common side (a leg), segment NL, and we know that the hypotenuses are congruent, the two triangles are congruent by HL. Remember that means that all corresponding sides and angles are con ...
Conjectures
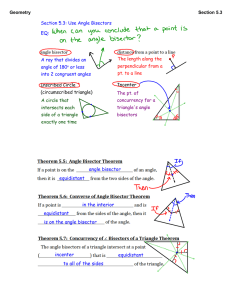
... If a triangle is isosceles, then its base angles are congruent. Converse of the Isosceles Triangle Conjecture If a triangle has two congruent base angles, then it is an isosceles triangle. Vertex Angle Bisector Conjecture In an isosceles triangle, the bisector of the vertex angle is also the altitud ...
... If a triangle is isosceles, then its base angles are congruent. Converse of the Isosceles Triangle Conjecture If a triangle has two congruent base angles, then it is an isosceles triangle. Vertex Angle Bisector Conjecture In an isosceles triangle, the bisector of the vertex angle is also the altitud ...























