More on Neutral Geometry I (Including Section 3.3) ( "NIB" means
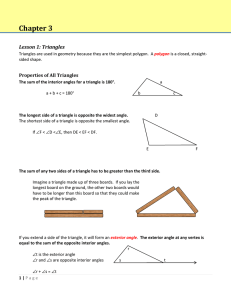
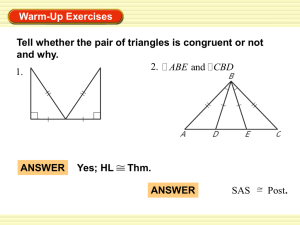
... Theorem 3.3.3 (Angle-Angle-Side Congruence Condition): If, in two triangles, the vertices of one triangle can be put into one-to-one correspondence with the vertices of the other triangle such that: Two angles and the side opposite one of them in one triangle are congruent to the corresponding angle ...
... Theorem 3.3.3 (Angle-Angle-Side Congruence Condition): If, in two triangles, the vertices of one triangle can be put into one-to-one correspondence with the vertices of the other triangle such that: Two angles and the side opposite one of them in one triangle are congruent to the corresponding angle ...
Practical Geometry
... In the above construction, lengths of two sides and measure of one angle were given. Now study the following problems: In ΔABC, if AB = 3cm, AC = 5 cm and m∠C = 30°. Can we draw this triangle? We may draw AC = 5 cm and draw ∠C of measure 30°. CA is one arm of ∠C. Point B should be lying on the other ...
... In the above construction, lengths of two sides and measure of one angle were given. Now study the following problems: In ΔABC, if AB = 3cm, AC = 5 cm and m∠C = 30°. Can we draw this triangle? We may draw AC = 5 cm and draw ∠C of measure 30°. CA is one arm of ∠C. Point B should be lying on the other ...
HighSchoolMath_revie..
... We use a right angled triangle to consider the Trig. Ratio and we remember that the Ratio of Corresponding Sides in Similar Triangles remains constant. Given a triangle ABC we denote the lengths of the sides to be a,b and c. There are 6 Ratios and are defined as follows: 3 MAJOR and 3 MINOR ...
... We use a right angled triangle to consider the Trig. Ratio and we remember that the Ratio of Corresponding Sides in Similar Triangles remains constant. Given a triangle ABC we denote the lengths of the sides to be a,b and c. There are 6 Ratios and are defined as follows: 3 MAJOR and 3 MINOR ...