2.6 Lecture Note
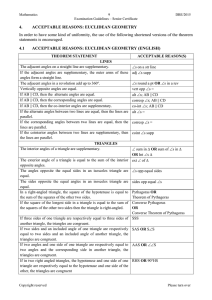
... 2. A total of $7000 is invested in two simple interest accounts. On one account the annual simple interest rate is 7.5%, and on the second account the annual simple interest rate is 10%. How much should be invested in each account so that the annual interest earned by each account is the same? ...
... 2. A total of $7000 is invested in two simple interest accounts. On one account the annual simple interest rate is 7.5%, and on the second account the annual simple interest rate is 10%. How much should be invested in each account so that the annual interest earned by each account is the same? ...
MONTH (Teacher would insert the month they are mapping)
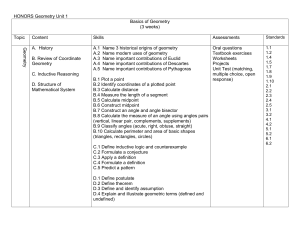
... Pythagorean Theorem B.2 Prove the Pythagorean Theorem B.3 Classify right triangles as acute, right, or obtuse using the Converse of the Pythagorean Theorem B.4 Solve real-world problems using the Pythagorean Theorem C.1 Find the missing side lengths of a 45-45-90 triangle C.2 Find the missing side l ...
... Pythagorean Theorem B.2 Prove the Pythagorean Theorem B.3 Classify right triangles as acute, right, or obtuse using the Converse of the Pythagorean Theorem B.4 Solve real-world problems using the Pythagorean Theorem C.1 Find the missing side lengths of a 45-45-90 triangle C.2 Find the missing side l ...
TOPIC #2-1: EXPLORING SIMILAR POLYGONS
... a) Quad EFGH Quad _________________. b) What is their common ratio?_____________ c) Find the following: ...
... a) Quad EFGH Quad _________________. b) What is their common ratio?_____________ c) Find the following: ...
Key Understandings
... -Mr. x 2 wants to party to all of his buddies have to come over (every term comes to the side with x 2 ) -Once everybody comes over, Mr. x 2 parties by playing with bubbles (once every term is on one side, FACTOR) *Don’t forget the T-Chart! When in doubt, set things equal to each other When given le ...
... -Mr. x 2 wants to party to all of his buddies have to come over (every term comes to the side with x 2 ) -Once everybody comes over, Mr. x 2 parties by playing with bubbles (once every term is on one side, FACTOR) *Don’t forget the T-Chart! When in doubt, set things equal to each other When given le ...
Notes on Proofs - Page 1 Name_________________________
... In order to construct a proper proof, one simply puts the thought process above into a clear and concise format. Let's first observe some characteristics about the thought process above. First, the student observed what was given. At the beginning of a formal Geometry proof, the given information is ...
... In order to construct a proper proof, one simply puts the thought process above into a clear and concise format. Let's first observe some characteristics about the thought process above. First, the student observed what was given. At the beginning of a formal Geometry proof, the given information is ...
Spring Review 2017 - Blue Valley Schools
... Simplify the following in simple radical form: a) 4 54 ...
... Simplify the following in simple radical form: a) 4 54 ...
9 Interior Angles of Polygons Lab-167v5vm
... By splitting any polygon into triangles you can find the sum of the interior angles of the polygon. 3. Using the splitting triangle method find the sum of the interior angles of this octagon. (If you did not do page one, you will get this wrong! Go back and read.) ...
... By splitting any polygon into triangles you can find the sum of the interior angles of the polygon. 3. Using the splitting triangle method find the sum of the interior angles of this octagon. (If you did not do page one, you will get this wrong! Go back and read.) ...