9 Interior Angles of Polygons Lab
... The quadrilateral is now divided into two triangles, Triangle DEG and Triangle FEG. Angles 1, 2, and 3 represent the interior angles of Triangle DEG and Angles 4, 5, and 6 represent the interior angles of Triangle FEG. ...
... The quadrilateral is now divided into two triangles, Triangle DEG and Triangle FEG. Angles 1, 2, and 3 represent the interior angles of Triangle DEG and Angles 4, 5, and 6 represent the interior angles of Triangle FEG. ...
(2) The student erred because the included the measures of angles
... (2) (2) The student erred because the included the measures of angles F, G, K, and N which are not angles of the polygon. Since these angles form a circle, the student can get the correct answer of 540 by subtracting 360 from the answer that they got. Another approach would be to divide the pentagon ...
... (2) (2) The student erred because the included the measures of angles F, G, K, and N which are not angles of the polygon. Since these angles form a circle, the student can get the correct answer of 540 by subtracting 360 from the answer that they got. Another approach would be to divide the pentagon ...
The sum of the interior angles of a triangle makes
... ACD + BCA = Two right angles Two angles on a straight line are either two right angles, or equal to two right angles. ...
... ACD + BCA = Two right angles Two angles on a straight line are either two right angles, or equal to two right angles. ...
Unit 1 lunch lines task day one
... How do you know that vertical angles are congruent? m∠1 + m∠3 = 180° because of the Linear Pair postulate m∠2 + m∠3 = 180° because of the Linear Pair postulate Set the two equations equal to each other since they both equal 180 degrees. m∠2 + m∠3 = m∠1 + m∠3 m∠3 m∠3 m∠2 = m∠1 ...
... How do you know that vertical angles are congruent? m∠1 + m∠3 = 180° because of the Linear Pair postulate m∠2 + m∠3 = 180° because of the Linear Pair postulate Set the two equations equal to each other since they both equal 180 degrees. m∠2 + m∠3 = m∠1 + m∠3 m∠3 m∠3 m∠2 = m∠1 ...
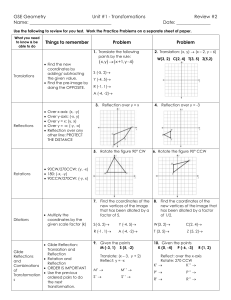
Name: Date:
... Base Angles -If 2 sides in a triangle are congruent, then the angles opposite them are congruent. ...
... Base Angles -If 2 sides in a triangle are congruent, then the angles opposite them are congruent. ...
GTPS Curriculum – Geometry 3 weeks Topic: 1
... G-SRT.1b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G-SRT.2. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity ...
... G-SRT.1b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G-SRT.2. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity ...