Maths Prilim Pages Book II New.pmd
... Step 1: Draw a ray AC making an acute angle with AB. Step 2: Starting with A, mark off 5 points C1, C2, C3, C4 and C5 on AC at equal distances from the point A. Step 3: Join C5 and B. Step 4: Through C2 (i.e. the second point), draw C2D parallel to C5B meeting AB in D. ...
... Step 1: Draw a ray AC making an acute angle with AB. Step 2: Starting with A, mark off 5 points C1, C2, C3, C4 and C5 on AC at equal distances from the point A. Step 3: Join C5 and B. Step 4: Through C2 (i.e. the second point), draw C2D parallel to C5B meeting AB in D. ...
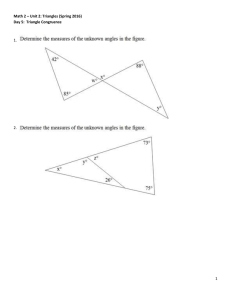
Math 2 – Unit 2: Triangles (Spring 2016) Day 5: Triangle
... Use the given information to mark the diagram and any additional congruence you can determine from the diagram. Then complete the triangle congruence statement and give the reason for triangle congruence . ...
... Use the given information to mark the diagram and any additional congruence you can determine from the diagram. Then complete the triangle congruence statement and give the reason for triangle congruence . ...
o Apply geometric concepts in modeling situations
... Set up and solve proportions based on similar figures and right triangles with altitudes. ...
... Set up and solve proportions based on similar figures and right triangles with altitudes. ...
Supp A - Penn Math
... If our classroom has concrete block walls, we could measure each child's height in "concrete block" units by asking each to stand against the wall and counting blocks until we came to the top of the child's head. In this case, we would probably observe a drawback to our measuring technique. In all l ...
... If our classroom has concrete block walls, we could measure each child's height in "concrete block" units by asking each to stand against the wall and counting blocks until we came to the top of the child's head. In this case, we would probably observe a drawback to our measuring technique. In all l ...
4.1: Congruent Figures
... If two sides and the angle between them of one triangle are congruent to two sides and the angle between them of another triangle, the triangles are congruent ...
... If two sides and the angle between them of one triangle are congruent to two sides and the angle between them of another triangle, the triangles are congruent ...