Taxicab Triangle Incircles and Circumcircles
... Figure 2: Inscribed taxicab angles. The angles shown are a) strictly positively inscribed, b) completely inscribed, and c) strictly negatively inscribed Definition 2.1 A taxicab angle is positively inscribed if a line of slope 1 through its vertex remains outside the angle. Definition 2.2 A taxicab ...
... Figure 2: Inscribed taxicab angles. The angles shown are a) strictly positively inscribed, b) completely inscribed, and c) strictly negatively inscribed Definition 2.1 A taxicab angle is positively inscribed if a line of slope 1 through its vertex remains outside the angle. Definition 2.2 A taxicab ...
Unit 5 - Geometry - CMS Secondary Math Wiki
... Standard: Standard: G.CO.9 -- Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are ex ...
... Standard: Standard: G.CO.9 -- Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are ex ...
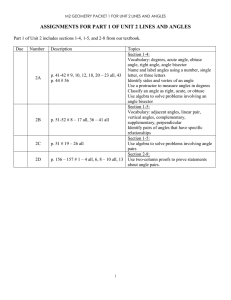
Packet 1 for Unit 2 M2 Geo
... Angles that have the same measure are congruent angles. A ray that divides an angle into two congruent angles is is the angle bisector called an angle bisector. In Figure 4, of ∠ MPR, and ∠ MPN ≅ ∠ NPR. Point N is in the interior of ...
... Angles that have the same measure are congruent angles. A ray that divides an angle into two congruent angles is is the angle bisector called an angle bisector. In Figure 4, of ∠ MPR, and ∠ MPN ≅ ∠ NPR. Point N is in the interior of ...
Postulates - cloudfront.net
... Postulate 20 Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent. Postulate 21 ...
... Postulate 20 Side-Angle-Side (SAS) Congruence Postulate: If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent. Postulate 21 ...
Geometry 21 - Fairfield Public Schools
... an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)2 as 5 minus a positive number times a square and use that to realize that its value cannot be more ...
... an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects. For example, they can see 5 – 3(x – y)2 as 5 minus a positive number times a square and use that to realize that its value cannot be more ...
The Extraordinary Sums of Leonhard Euler
... Step 1: Put the compass point on point P. Draw arcs intersecting l in two points. Label the points A and B. Step 2: Open the compass wider. With the compass tip on A, draw an arc above point P. Step 3: With the same compass setting, put the compass point on point B. Draw an arc that intersects the a ...
... Step 1: Put the compass point on point P. Draw arcs intersecting l in two points. Label the points A and B. Step 2: Open the compass wider. With the compass tip on A, draw an arc above point P. Step 3: With the same compass setting, put the compass point on point B. Draw an arc that intersects the a ...