Squaring The Circle In The Hyperbolic Disk - Rose
... the circle, could be constructed in hyperbolic geometry. Without a model or even a distance formula, he reasoned a way to construct circles and regular quadrilaterals with the same hyperbolic areas. At that time, constructing a Euclidean square with the same area as a given circle was an open proble ...
... the circle, could be constructed in hyperbolic geometry. Without a model or even a distance formula, he reasoned a way to construct circles and regular quadrilaterals with the same hyperbolic areas. At that time, constructing a Euclidean square with the same area as a given circle was an open proble ...
Regular Polygons
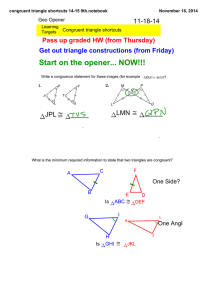
... 3. Use the angle measures to calculate the unknown angles in each triangle. NOTE: The following are not to scale. Use calculations rather than a protractor to solve. ...
... 3. Use the angle measures to calculate the unknown angles in each triangle. NOTE: The following are not to scale. Use calculations rather than a protractor to solve. ...
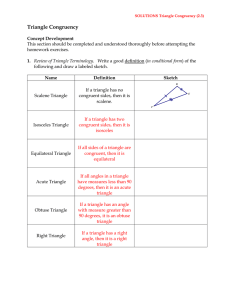
Chapter 6 Blank Conjectures
... The line of reflection is the ______________ _____________ of every segment joining a point in the original figure with its image. ...
... The line of reflection is the ______________ _____________ of every segment joining a point in the original figure with its image. ...
Math Grade 4 Sampler - Common Core Standards Plus
... with arrows at both ends. Typically two points are labeled on the line, so we call the line by those two points. Line AB is a line with arrows at each end, and two points labeled A and B. Notice that there are two ways to write the name for a line. A line segment is a part of a line. When a line seg ...
... with arrows at both ends. Typically two points are labeled on the line, so we call the line by those two points. Line AB is a line with arrows at each end, and two points labeled A and B. Notice that there are two ways to write the name for a line. A line segment is a part of a line. When a line seg ...
Circles - AGMath.com
... Solve the following word problems involving Pi and speed: 1. The radius of the Earth at the equator is 3,963 miles. The earth makes one rotation every 24 hours. If you are standing on the equator, you are spinning around the Earth at a very high speed. Standing on the poles, you are only rotating. H ...
... Solve the following word problems involving Pi and speed: 1. The radius of the Earth at the equator is 3,963 miles. The earth makes one rotation every 24 hours. If you are standing on the equator, you are spinning around the Earth at a very high speed. Standing on the poles, you are only rotating. H ...
geometry pacing guide - Kalispell Public Schools
... Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motions. CONGRUENCE: Prove geometric theorems. CC.9-12.G.CO.10 Prove theorems about triangles. ...
... Explain how the criteria for triangle congruence (ASA, SAS, and SSS) follow from the definition of congruence in terms of rigid motions. CONGRUENCE: Prove geometric theorems. CC.9-12.G.CO.10 Prove theorems about triangles. ...