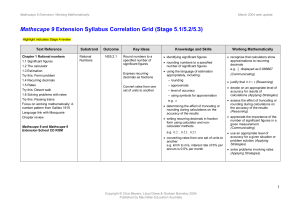
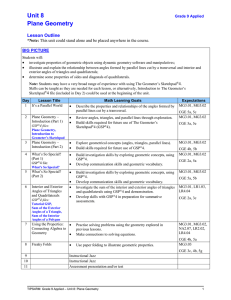
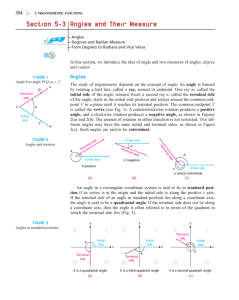
Objective(s) - Shelby County Schools
... Teachers are expected to carefully craft weekly and daily learning objectives/ based on their knowledge of TEM Teach 1. In addition, teachers should include related best practices based upon the TN State Standards, related shifts, and knowledge of students from a variety of sources (e.g., student wo ...
... Teachers are expected to carefully craft weekly and daily learning objectives/ based on their knowledge of TEM Teach 1. In addition, teachers should include related best practices based upon the TN State Standards, related shifts, and knowledge of students from a variety of sources (e.g., student wo ...
Dissection of a triangle into similar triangles
... Let P and P 0 be polygons in the Euclidean plane. A dissection (tiling) of P into P 0 is a decomposition of P into finitely many, internally disjoint polygons P 10 , ..., Pn0 (n ≥ 2) such that all of the Pi0 are similar to P 0 . A dissection is perfect if the Pi0 are pairwise incongruent. The perfec ...
... Let P and P 0 be polygons in the Euclidean plane. A dissection (tiling) of P into P 0 is a decomposition of P into finitely many, internally disjoint polygons P 10 , ..., Pn0 (n ≥ 2) such that all of the Pi0 are similar to P 0 . A dissection is perfect if the Pi0 are pairwise incongruent. The perfec ...
Investigating Geometry Activity: The Transitive Property of Parallel
... formed that is 498 and the one below it are supplementary. So, the angle below it is 1318. Since line n intersects line j, the angle formed that is 1318 and the one above it are supplementary. So, the angle above it is 498. Since a pair of corresponding angles are congruent, the lines m and n are pa ...
... formed that is 498 and the one below it are supplementary. So, the angle below it is 1318. Since line n intersects line j, the angle formed that is 1318 and the one above it are supplementary. So, the angle above it is 498. Since a pair of corresponding angles are congruent, the lines m and n are pa ...
DIVIDING AN ANGLE INTO EQUAL PARTS
... for dividing the angle 360◦ into n equal parts. The angle (360/n)◦ is the exterior angle of a regular n-sided polygon and so such a polygon can be constructed. Hence, by the result quoted above, n must have the form 2k for an integer k or the form 2m p1 · · · pr where p1 , . . . , pr are distinct Fe ...
... for dividing the angle 360◦ into n equal parts. The angle (360/n)◦ is the exterior angle of a regular n-sided polygon and so such a polygon can be constructed. Hence, by the result quoted above, n must have the form 2k for an integer k or the form 2m p1 · · · pr where p1 , . . . , pr are distinct Fe ...