Course Title: Geometry Grade: 8 Level: Honors I. Course Description
... Course Description/Overview This course begins with an informal introduction to geometry, experimenting with drawings, constructions, and geometry software. Using a theme of investigation before formalization, the course examines congruence, similarity, parallel and perpendicular lines, the properti ...
... Course Description/Overview This course begins with an informal introduction to geometry, experimenting with drawings, constructions, and geometry software. Using a theme of investigation before formalization, the course examines congruence, similarity, parallel and perpendicular lines, the properti ...
Family Letter 8
... Lines also have special relationships. Intersecting lines that form right angles are called perpendicular lines. Lines that are in the same plane, but do not cross, are called parallel lines. If two parallel lines are cut by a third line, or a transversal, all of the acute angles are congruent and a ...
... Lines also have special relationships. Intersecting lines that form right angles are called perpendicular lines. Lines that are in the same plane, but do not cross, are called parallel lines. If two parallel lines are cut by a third line, or a transversal, all of the acute angles are congruent and a ...
Geometry - Perfection Learning
... congruent; the diagonals of a parallelogram bisect each other; and rectangles are parallelograms with congruent diagonals. Prove that given quadrilaterals are parallelograms, rhombuses, rectangles, squares or trapezoids. Include coordinate proofs of quadrilaterals in the coordinate plane. Find measu ...
... congruent; the diagonals of a parallelogram bisect each other; and rectangles are parallelograms with congruent diagonals. Prove that given quadrilaterals are parallelograms, rhombuses, rectangles, squares or trapezoids. Include coordinate proofs of quadrilaterals in the coordinate plane. Find measu ...
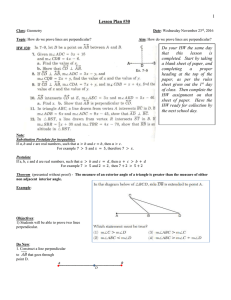
Geometry 1-4 Angle Measure A. Definitions 1. Astronomer Claudius
... 4. Angles that have the same measure are said to be congruent angles. Example 3: Find the value of x and ∠ABC . ...
... 4. Angles that have the same measure are said to be congruent angles. Example 3: Find the value of x and ∠ABC . ...
m3hsoln2.tex M3H SOLUTIONS 2. 3.2.2017 Q1 (Angle at centre
... ∠OCA = θ, ∠OBA = φ. So AB subtends ∠ACB = θ + φ at the circumference. In ∆AOC, ∠AOC = π − 2θ (angle sum is π), and similarly ∠BOC = π − 2φ. The three angles are O sum to 2π; the two just mentioned sum to 2π − 2θ − 2φ. So ∠AOC = 2(θ + φ) = 2.∠ACB. // Note that if the chord goes through the centre, th ...
... ∠OCA = θ, ∠OBA = φ. So AB subtends ∠ACB = θ + φ at the circumference. In ∆AOC, ∠AOC = π − 2θ (angle sum is π), and similarly ∠BOC = π − 2φ. The three angles are O sum to 2π; the two just mentioned sum to 2π − 2θ − 2φ. So ∠AOC = 2(θ + φ) = 2.∠ACB. // Note that if the chord goes through the centre, th ...