Download Chapter 5 – Plane Geometry

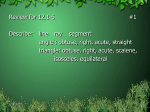
Chapter 5 – Plane Geometry
5-1 Points, Lines, Planes, and Angles
5-2 Parallel and Perpendicular Lines
5-3 Triangles
5-4 Polygons
5-5 Coordinate Geometry
5-6 Congruence
5-7 Transformations
5-8 Symmetry
5-9 Tessellations
5-1 Points, Lines, Planes & Angles
Vocabulary
 Point – Names a location
 Line – Perfectly straight and extends in
both directions forever
 Plane - Perfectly flat surface that extends
forever in all directions
 Segment – Part of a line between two
points
 Ray – Part of a line that starts at a point
and extends forever in one direction
Point
Line
Segment
Ray
Example 1
•
•
•
•
•
Name four points
Name the line
Name the plane
Name four segments
Name five rays
More Vocabulary
Right Angle – Measures exactly 90°
 Acute Angle – Measures less than 90 °
 Obtuse Angle – Measures more than 90 °
 Complementary Angle – Angles that
measure 90 ° together
 Supplementary Angle – Angles that
measure 180 ° together

Right Angle
Acute Angle
Obtuse Angle
Complementary Angle
Supplementary Angle
Example 2
•
•
•
•
•
Name the following:
Right Angle
Acute Angle
Obtuse Angle
Complementary Angle
• Supplementary Angle
Even MORE Vocabulary
 Congruent – Figures that have the same
size AND shape

Vertical Angles



Angles A & C are VA
Angles B & D are VA
If Angle A is 60° what is the measure of
angle B?
Homework/Classwork
Page 225, #13-34
5-2 Parallel and Perpendicular Lines
Vocabulary
 Parallel Lines – Two lines in a plane that
never meet, ex. Railroad Tracks
 Perpendicular Lines – Lines that
intersect to form Right Angles
 Transversal – A line that intersects two
or more lines at an angle other than a
Right Angle
Parallel Lines
Perpendicular Lines
Transversal

Transversals to parallel lines have
interesting properties

The color coded numbers are congruent
Properties of Transversals to Parallel Lines

If two parallel lines are intersected by a
transversal:




The acute angles formed are all congruent
The obtuse angles are all congruent
And any acute angle is supplementary to any
obtuse angle
If the transversal is perpendicular to the
parallel lines, all of the angles formed are
congruent 90° angles
Alternate Interior Angles
Alternate Exterior Angles
Corresponding Angles
Symbols

Parallel

Perpendicular

Congruent

Example 1

In the figure Line X
Y

Find each angle measure

In the figure Line A
B

Find each angle measure
Homework/Classwork
Page
230, # 6-20
5-3 Triangles

Triangle Sum Theorem – The angle measures
of a triangle in a plane add to 180°

Because of alternate interior angles, the following is true:
m1  m2  m  180
m1  m4
m3  m5
Vocabulary

Acute Triangle – All angles are less than
90°

Right Triangle – Has one 90° angle

Obtuse Triangle – Has one obtuse angle
Example

Find the missing angle
Example

Find the missing angle.
Example

Find the missing angles
Vocabulary

Equilateral Triangle – 3 congruent sides
and angles

Isosceles Triangle – 2 congruent sides
and angles

Scalene Triangle – No congruent sides
or angles

Equilateral Triangle

Isosceles Triangle

Scalene Triangle
Remember…they are ALL triangles
Example

Find the missing angle(s)
Example

Find the missing angle(s)
Example

Find the missing angle(s)
Example

Find the angles. Hint, remember the
triangle sum theorem
Classwork/Homework
Page
237, #10-26
5-4 Polygons

Polygons



Have 3 or more sides
Named by the number
of sides
“Regular Polygon”
means that all the sides
are equal length
Polygon
Triangle
# of
Sides
3
Quadrilateral
4
Pentagon
5
Hexagon
6
Heptagon
7
Octagon
8
n-gon
n
Finding the sum of angles in a polygon

Step 1:

Divide the polygon into triangles with common
vertex

Step 2:

Multiply the number of triangles by 180
The Short Cut
180°(n – 2) where
n = the number of
angles in the figure
 In this case n = 6
 = 180°(6 – 2)
 = 180°(4)
 = 720°

*Notice that n - 2 = 4
**Also notice that the figure can be
broken into 4 triangles…coincidence?
I don’t think so!
Example

Find the missing angle
This chart may help…
Polygon
Total
Angle
measure
Triangle
# of
Sides
3
Quadrilateral
4
360°
Pentagon
5
540°
Hexagon
6
720°
Heptagon
7
900°
Octagon
8
1080°
n-gon
n
n°
180°
Classwork/Homework
Page
242, # 13-24