2-6 - My CCSD
... 1. Given 2. Def. Cong. Angles 3. Def. Cong. Angles 4. Transitive property 5. Def. Cong. Angles ...
... 1. Given 2. Def. Cong. Angles 3. Def. Cong. Angles 4. Transitive property 5. Def. Cong. Angles ...
Geometry Yearlong Curriculum Map
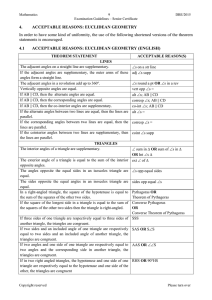
... G-GPE.4 Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, ...
... G-GPE.4 Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, ...
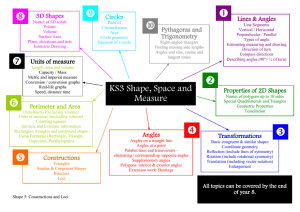
KS3 Shape 5 Constructions and loci 53.77KB
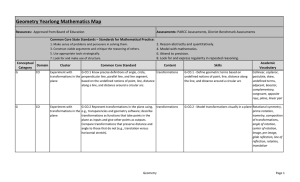
... Required: Ruler, angle measurer or protractor Ensure students are required to measure and draw line segments in both centimetres (eg 3.4 centimetres) and millimetres (eg 34 millimetres) and stretch them to make judgements on even more precise measurements such as (34.5 millimetres). The accuracy of ...
... Required: Ruler, angle measurer or protractor Ensure students are required to measure and draw line segments in both centimetres (eg 3.4 centimetres) and millimetres (eg 34 millimetres) and stretch them to make judgements on even more precise measurements such as (34.5 millimetres). The accuracy of ...
6-12 Comp 3 trainer notes - Math6-12TestPrep
... 3 Knowledge of geometry from a synthetic perspective 1. Determine the change in the area or volume of a figure when its dimensions are altered. 2. Estimate measurements of familiar objects using metric or standard units. 3. Determine the relationships between points, lines, and planes, including the ...
... 3 Knowledge of geometry from a synthetic perspective 1. Determine the change in the area or volume of a figure when its dimensions are altered. 2. Estimate measurements of familiar objects using metric or standard units. 3. Determine the relationships between points, lines, and planes, including the ...
Section 8A – Angles and Circles
... • The complement of an angle whose measure is θ is an angle whose measure is π 2 − θ. • The supplement of an angle whose measure is θ is an angle whose measure is π − θ. Example 5. Sketch and label an obtuse angle θ in standard position and its supplement α. ...
... • The complement of an angle whose measure is θ is an angle whose measure is π 2 − θ. • The supplement of an angle whose measure is θ is an angle whose measure is π − θ. Example 5. Sketch and label an obtuse angle θ in standard position and its supplement α. ...
Eight circle theorems page
... [This is a weird theorem, and needs a bit more explanation: Chord DF splits the circle into two segments. In one segment, there is an angle, β, 'facing' the chord, DF – this segment is called the alternate segment. Partly in the other segment, and partly outside the circle altogether, the angle α, i ...
... [This is a weird theorem, and needs a bit more explanation: Chord DF splits the circle into two segments. In one segment, there is an angle, β, 'facing' the chord, DF – this segment is called the alternate segment. Partly in the other segment, and partly outside the circle altogether, the angle α, i ...