Downloadable PDF - Rose
Downloadable PDF - Rose

... P(n,0) to the analogous side in P(n,n) is the same, and is equal to r. With out loss of generality, we can now select segment A0P from triangle A0B0P. That segment is the hypotenuse of the right triangle A0A1P. So, the product of the length of segment A0P and the sin of angle B0A0P is, by right tria ...
Angles
Angles

Iterated Perpendicular Constructions from Interior Points on N-gons
Iterated Perpendicular Constructions from Interior Points on N-gons

Congruent Triangles
Congruent Triangles

360
360

7-3-formulas-involving-polygons-ppt
7-3-formulas-involving-polygons-ppt

Notes Section 2.5 and 2.7
Notes Section 2.5 and 2.7

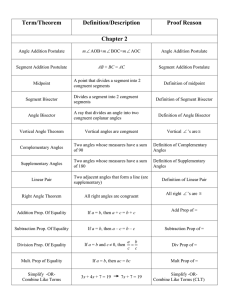
Term/Theorem
Term/Theorem

Reasoning in Geometry
Reasoning in Geometry

CLASSROOM COPY – DO NOT WRITE ON THIS! CRS PPF 703
CLASSROOM COPY – DO NOT WRITE ON THIS! CRS PPF 703

Triangle Congruence
Triangle Congruence

Circle Geometry
Circle Geometry

3-3 Proving Lines Parallel 3
3-3 Proving Lines Parallel 3

6-6 Notes - Blair Schools
6-6 Notes - Blair Schools

Name: _______________________ Date: ____ Period:____ Similar Triangles: Day 1
Name: _______________________ Date: ____ Period:____ Similar Triangles: Day 1

The discovery of non-Euclidean geometries
The discovery of non-Euclidean geometries

4-2 Angle Relationships in Triangles 4-2 Angle
4-2 Angle Relationships in Triangles 4-2 Angle

Section 2-5: Proving Angles Congruent
Section 2-5: Proving Angles Congruent

Geometry Refresher
Geometry Refresher

Section:
Section:

... reason why (SSS, SAS, ASA or AAS). Be sure to mark the pictures with information you know. A. ...
Tricky Triangles - Etiwanda E
Tricky Triangles - Etiwanda E

Math 2 Lesson Plan - GSE ANALYTIC GEOMETRY
Math 2 Lesson Plan - GSE ANALYTIC GEOMETRY

We are dismissed early if there is a teacher`s meeting
We are dismissed early if there is a teacher`s meeting

Activity 4 Angles of a Triangle - TI Education
Activity 4 Angles of a Triangle - TI Education

HERE
HERE

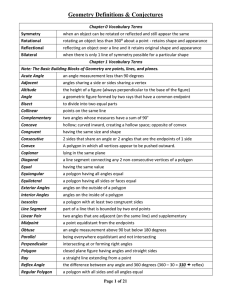
... By definition, two polygons are similar if and only if their corresponding angles are congruent and their corresponding side lengths are proportional. Thus, similar figures may have different sizes, but they have the same shape. The following foci incorporate a variety of approaches (geometric, grap ...

Rational trigonometry

Rational trigonometry is a proposed reformulation of metrical planar and solid geometries (which includes trigonometry) by Canadian mathematician Norman J. Wildberger, currently an associate professor of mathematics at the University of New South Wales. His ideas are set out in his 2005 book Divine Proportions: Rational Trigonometry to Universal Geometry. According to New Scientist, part of his motivation for an alternative to traditional trigonometry was to avoid some problems that occur when infinite series are used in mathematics. Rational trigonometry avoids direct use of transcendental functions like sine and cosine by substituting their squared equivalents. Wildberger draws inspiration from mathematicians predating Georg Cantor's infinite set-theory, like Gauss and Euclid, who he claims were far more wary of using infinite sets than modern mathematicians. To date, rational trigonometry is largely unmentioned in mainstream mathematical literature.