Remedial - MoreMaths
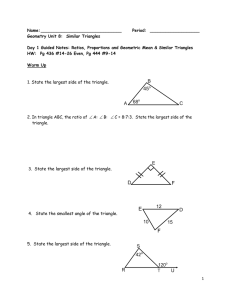
... If any two triangles, ΔABC and ΔPQR are congruent under the correspondence ABC QRP, then A = Q, B = R, C = P, and ̅̅̅̅= ̅̅̅̅, ̅̅̅̅ = ̅̅̅̅ and ̅̅̅̅ = ̅̅̅̅ . ...
... If any two triangles, ΔABC and ΔPQR are congruent under the correspondence ABC QRP, then A = Q, B = R, C = P, and ̅̅̅̅= ̅̅̅̅, ̅̅̅̅ = ̅̅̅̅ and ̅̅̅̅ = ̅̅̅̅ . ...
Tasks on SketchPad
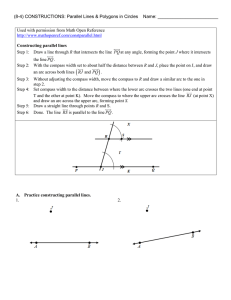
... 1. Create a point on the perpendicular bisector. To do this, select the Point Tool and move the cursor onto the line, which will highlight in blue. 2. Select the Arrow Tool, and then click on the perpendicular bisector. It will highlight in purple. At this point, if you hit the delete key to remove ...
... 1. Create a point on the perpendicular bisector. To do this, select the Point Tool and move the cursor onto the line, which will highlight in blue. 2. Select the Arrow Tool, and then click on the perpendicular bisector. It will highlight in purple. At this point, if you hit the delete key to remove ...
elementary montessori geometry album
... Knowledge from Manipulation of Figures, Solid and Plane A Solid cannot be in two places at the same time A Solid as a state of matter Geometric Solid (three-dimensional) The surface of a solid The surface of a solid, the line and the point in the solid: from the solid to the point The point, the lin ...
... Knowledge from Manipulation of Figures, Solid and Plane A Solid cannot be in two places at the same time A Solid as a state of matter Geometric Solid (three-dimensional) The surface of a solid The surface of a solid, the line and the point in the solid: from the solid to the point The point, the lin ...
grade 5 supplement - The Math Learning Center
... 2. Ask students to make a small dot at point (3, 3). Invite a volunteer to show (3, 3) on the display Coordinate Grid. You may need to remind students to count along the x-axis first and then along the y-axis to locate the point. Explain that this dot is what mathematicians call a point. A point is ...
... 2. Ask students to make a small dot at point (3, 3). Invite a volunteer to show (3, 3) on the display Coordinate Grid. You may need to remind students to count along the x-axis first and then along the y-axis to locate the point. Explain that this dot is what mathematicians call a point. A point is ...