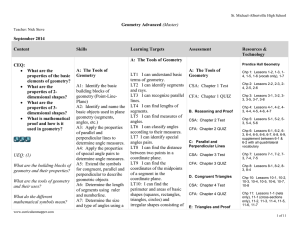
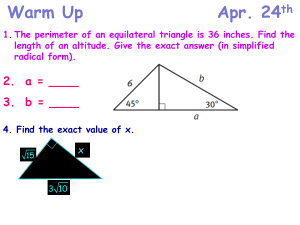
Euclidean
... two straight lines meeting within the triangle, the straight lines so constructed will be less than the remaining two sides of the triangle, but will contain a greater angle. Proposition 22. Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it ...
... two straight lines meeting within the triangle, the straight lines so constructed will be less than the remaining two sides of the triangle, but will contain a greater angle. Proposition 22. Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it ...
1.2 Euclid`s Parallel Postulate - Department of Mathematical Sciences
... appear to provide a good foundation, in fact they ultimately raise more questions than they answer. To use them we must first be able to work with terms like “part,” “breadthless,” “length,” “evenly with,” and we find that attempting to define these terms leads us even further backwards to yet more ...
... appear to provide a good foundation, in fact they ultimately raise more questions than they answer. To use them we must first be able to work with terms like “part,” “breadthless,” “length,” “evenly with,” and we find that attempting to define these terms leads us even further backwards to yet more ...