Notes 8C Proving Triangles similar.notebook
... 1. Write a Similarity Statement and similarity ratio. F ...
... 1. Write a Similarity Statement and similarity ratio. F ...
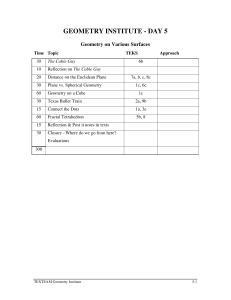
Math Institute April 2010 Most Missed Questions: Applying Basic
... Properties of SIMILAR TRIANGLES Reflection: One triangle can be the mirror image of the other, but as long as they are the same shape, the triangles are still similar. It can be reflected in any direction, up, down, left, right. ...
... Properties of SIMILAR TRIANGLES Reflection: One triangle can be the mirror image of the other, but as long as they are the same shape, the triangles are still similar. It can be reflected in any direction, up, down, left, right. ...
understand similarity in terms of similarity transformations
... they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. MCC9-12.G.SRT.3 Use the properties of similarity transformations to establish the AA cr ...
... they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. MCC9-12.G.SRT.3 Use the properties of similarity transformations to establish the AA cr ...
Slide 1
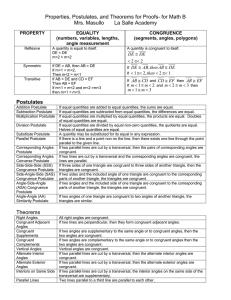
... If three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent. If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. If two angles and the included side of one tria ...
... If three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent. If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. If two angles and the included side of one tria ...