4-7
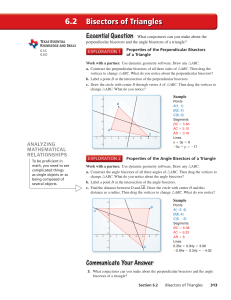
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
Introduction to Proof
... This is false, because a rectangle that is not a square constitutes a counter-example: all its angles are congruent, and yet all the sides are not congruent. Proving Something is True Conjectures can be proved true by using a logical argument, based on known facts. When a conjecture has been proved ...
... This is false, because a rectangle that is not a square constitutes a counter-example: all its angles are congruent, and yet all the sides are not congruent. Proving Something is True Conjectures can be proved true by using a logical argument, based on known facts. When a conjecture has been proved ...